题目内容
6.已知直线l:y=-2x+2与x轴、y轴交于A、B两点,平移直线l交y=$\frac{k}{x}$于C、D两点,且CD=2AB,若AC=5,则k=16.分析 先由直线l:y=-2x+2与x轴、y轴交于A,B两点,求出A(1,0),B(0,2),得出OA=1,OB=2,
由△AOB∽△CED,得出DE=4,CE=2,设D(a,b),则C(a+2,b-4),根据反比例函数图象上点的坐标特征得出ab=(a+2)(b-4),得出b=4+2a①,在RT△ACM中,根据勾股定理得出A(a+1)2+(b-4)2=52,得出a2+b2+2a-8b=8②,把①代入②得到关于a的方程,解方程确定a的值,从而确定k的值.
解答 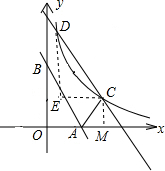 解:如图,∵直线l:y=-2x+2与x轴y轴交于A,B两点,
解:如图,∵直线l:y=-2x+2与x轴y轴交于A,B两点,
∴当x=0时,y=2;y=0时,-2x+2=0,x=1;
∴A(1,0),B(0,2),
∴OA=1,OB=2,
∵△AOB∽△CED,
∴$\frac{DE}{OB}$=$\frac{CE}{OA}$=$\frac{CD}{AB}$
∵CD=2AB,
∴DE=4,CE=2,
设D(a,b),则C(a+2,b-4),
∴ab=(a+2)(b-4),
化简得b=4+2a①,
在RT△ACM中,AM=a+2-1=a+1,CM=B-4,
∴AC2=(a+1)2+(b-4)2=52,
化简得,a2+b2+2a-8b=8②,
把①代入②得,a2+(4+2a)2-2a+8(4+2a)=8,
整理得,5a2+2a-24=0,
解得a1=2,a2=-$\frac{12}{5}$(舍去),
∴b=4+2×2=8,
∴k=ab=2×8=16.
故答案为16.
点评 本题考查了一次函数的图象与几何变换,三角形相似的性质以及勾股定理的应用,反比例函数图象上点的坐标特征,求得C、D的坐标是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
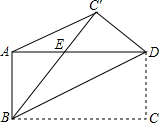 如图,将矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,连接AC′
如图,将矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,连接AC′
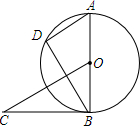 如图,⊙O的直径AB=6,BC切⊙O于B,OC∥AD,BC=4,求弦AD的长.
如图,⊙O的直径AB=6,BC切⊙O于B,OC∥AD,BC=4,求弦AD的长.