题目内容
15．化简$\frac{2}{x+1}$-$\frac{x-2}{{x}^{2}-1}$的结果是$\frac{x}{{x}^{2}-1}$．分析 原式两项通分并利用同分母分式的减法法则计算即可得到结果．
解答 解：原式=$\frac{2（x-1）}{（x+1）（x-1）}$-$\frac{x-2}{（x+1）（x-1）}$
=$\frac{2x-2-x+2}{（x+1）（x-1）}$
=$\frac{x}{{x}^{2}-1}$．
故答案为：$\frac{x}{{x}^{2}-1}$．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，数轴上有A、B、C、D四点，根据图中各点的位置，判断与10-2$\sqrt{39}$最接近的点是（ ）
10．
如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆，交弦AB于点D，连接CD，则阴影部分的面积为（ ）
如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆，交弦AB于点D，连接CD，则阴影部分的面积为（ ）| A． | π-1 | B． | 2π-1 | C． | $\frac{1}{2}$π-1 | D． | $\frac{1}{2}$π-2 |
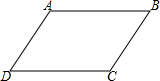（1）∵∠A+∠B=180°（已知）
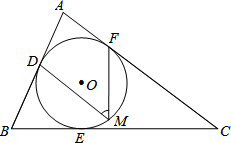如图，⊙O是△ABC的内切圆，点D、E、F为切点，点M为优弧DEF上任意一点，∠B=66°，∠C=37°，求∠M的大小．
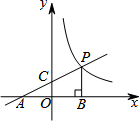如图，直线y1=$\frac{1}{2}$x+1分别交x轴，y轴于点A，C，点P是直线AC与双曲线y2=$\frac{k}{x}$（x＞0）在第一象限内的交点，PB⊥x轴于点B，△PAB的面积为4．
某公司投资1200万元购买了一条新生产线生产新产品．根据市场调研，生产每件产品需要成本50元，该产品进入市场后不得低于80元/件且不得超过160元/件，该产品销售量y（万件）与产品售价x（元）之间的关系如图所示．