题目内容
10.已知直线y=2x-k+3和直线y=3x+2k相交于点P,若点P在第一象限,且k是非负整数,则点P的坐标为(3,9).分析 联立两直线表达式成方程组可求出交点P的坐标,由点P在第一象限可得出关于k的一元一次不等式组,解之即可得出k的取值范围,结合k是非负整数可得出k=0,将其代入点P的坐标即可得出结论.
解答 解:联立两直线表达式成方程组,
$\left\{\begin{array}{l}{y=2x-k+3}\\{y=3x+2k}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=3-3k}\\{y=9-7k}\end{array}\right.$,
∴点P的坐标为(3-3k,9-7k).
∵点P在第一象限,
∴$\left\{\begin{array}{l}{3-3k>0}\\{9-7k>0}\end{array}\right.$,
解得:k<$\frac{9}{7}$.
∵k是非负整数,
∴k=0,
∴点P的坐标为(3,9).
故答案为:(3,9).
点评 本题考查了两条直线相交或平行问题、解二元一次不等式以及解一元一次不等式组,联立两直线表达式成方程组,通过解方程组求出交点P的坐标是解题的关键.

练习册系列答案
相关题目
5.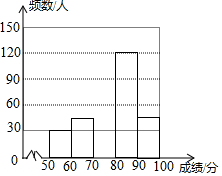 为了弘扬苏州优秀传统文化,某中学举办了苏州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分.赛后对全体参赛选手的成绩进行统计后,绘制了图中两幅不完整的答题情况的统计图.
为了弘扬苏州优秀传统文化,某中学举办了苏州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分.赛后对全体参赛选手的成绩进行统计后,绘制了图中两幅不完整的答题情况的统计图.
根据图中信息,解答下列问题:
(1)a=0.15,b=60;
(2)补全频数分布直方图;
(3)若绘制“答题情况的扇形统计图”,求成绩在“90≤x<100”组对应的扇形圆心角的度数.
 为了弘扬苏州优秀传统文化,某中学举办了苏州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分.赛后对全体参赛选手的成绩进行统计后,绘制了图中两幅不完整的答题情况的统计图.
为了弘扬苏州优秀传统文化,某中学举办了苏州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分.赛后对全体参赛选手的成绩进行统计后,绘制了图中两幅不完整的答题情况的统计图. | 成绩分组 (x/分) | 频数(人) | 频率 |
| 50≤x<60 | 30 | 0.10 |
| 60≤x<70 | 45 | a |
| 70≤x<80 | b | 0.20 |
| 80≤x<90 | 120 | 0.40 |
| 90≤x<100 | 45 | 0.15 |
(1)a=0.15,b=60;
(2)补全频数分布直方图;
(3)若绘制“答题情况的扇形统计图”,求成绩在“90≤x<100”组对应的扇形圆心角的度数.
 如图,在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=7,则点D到斜边AB的距离为7.
如图,在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=7,则点D到斜边AB的距离为7.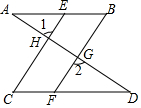 如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.
如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.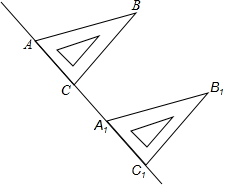 如图,同学们用直尺和三角板画平行线,将一块三角板ABC的一边AC贴着直尺推移到A1B1C1的位置.
如图,同学们用直尺和三角板画平行线,将一块三角板ABC的一边AC贴着直尺推移到A1B1C1的位置.