题目内容
19.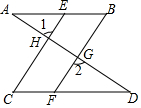 如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.
如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.证明:∵AB∥CD(已知)
∴∠B=∠BFD(两直线平行,内错角相等).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴BC∥BF(同位角相等,两直线平行)
∴∠2=∠CHG(两直线平行,同位角相等)
∵∠1=∠CHG(对顶角相等)
∴∠1=∠2(等量代换).
分析 欲证明∠1=∠2,只需推知BC∥BF即可.
解答 证明:∵AB∥CD(已知)
∴∠B=∠BFD( 两直线平行,内错角相等).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴BC∥BF(同位角相等,两直线平行)
∴∠2=∠CHG(两直线平行,同位角相等)
∵∠1=∠CHG(对顶角相等)
∴∠1=∠2(等量代换).
故答案是:∠BFD; 两直线平行,内错角相等; 等量代换;BC;BF;∠CHG;∠CHG; 对顶角相等.
点评 本题主要考查了平行线的判定与性质、对顶角相等、等量代换等知识,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列命题,其中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两点之间,垂线段最短 | |
| C. | 图形的平移改变了图形的位置和大小 | |
| D. | 三角形的一条中线能将三角形分成面积相等的两部分 |
11.下列计算正确的是( )
| A. | 2$\sqrt{3}+4\sqrt{2}=6\sqrt{5}$ | B. | $\sqrt{5}-\sqrt{2}=\sqrt{3}$ | C. | $\sqrt{2}(\sqrt{3}+\sqrt{5})=\sqrt{6}+\sqrt{10}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
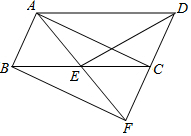 如图,在?ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.
如图,在?ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.