题目内容
 如图,直线y=
如图,直线y=| 4 |
| 3 |
| k |
| x |
| 4 |
| 3 |
| k |
| x |
| AO |
| BC |
考点:反比例函数与一次函数的交点问题,一次函数图象与几何变换
专题:计算题
分析:根据题意得到直线BC的解析式,根据直线AO和直线BC的解析式与双曲线y=
联立求得A、B的坐标,再由已知条件
=2,从而求出k值.
| k |
| x |
| AO |
| BC |
解答:解:∵将直线y=
x向下平移6个单位后得到直线BC,
∴直线BC解析式为:y=
x-6,
∵直线y=
x与双曲线y=
(x>0)交于点A,
∴A(
,
),
又∵直线y=
x-6与双曲线y=
(x>0)交于点B,且
=2,
∴B(
+
,
),将B的坐标代入y=
中,得
(
+
)
=k,
解得k=12.
故k值为12.
| 4 |
| 3 |
∴直线BC解析式为:y=
| 4 |
| 3 |
∵直线y=
| 4 |
| 3 |
| k |
| x |
∴A(
| ||
| 2 |
2
| ||
| 3 |
又∵直线y=
| 4 |
| 3 |
| k |
| x |
| AO |
| BC |
∴B(
| 9 |
| 2 |
| ||
| 4 |
| ||
| 3 |
| k |
| x |
(
| 9 |
| 2 |
| ||
| 4 |
| ||
| 3 |
解得k=12.
故k值为12.
点评:此题考查一次函数与反比例函数的性质,联立方程求出点的坐标,同时还考查学生的计算能力.

练习册系列答案
相关题目
 如图,在正方形网格中,角α、β、γ的大小关系是( )
如图,在正方形网格中,角α、β、γ的大小关系是( )| A、α>β>γ |
| B、α=β>γ |
| C、α<β=γ |
| D、α=β=γ |
 跳绳训练,随机选取48名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出频数分布表和频数分布直方图,(部分如图1所示),根据图表解答下列问题:
跳绳训练,随机选取48名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出频数分布表和频数分布直方图,(部分如图1所示),根据图表解答下列问题: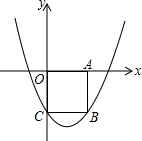 如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上,二次函数
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上,二次函数