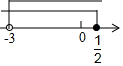
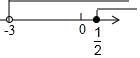
题目内容
11.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2017个图形中直角三角形的个数有( )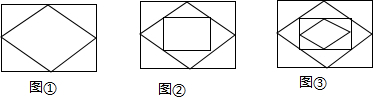
| A. | 8072个 | B. | 4036个 | C. | 4032个 | D. | 2016个 |
分析 观察图形可知,两个图形为一个组,直角三角形的个数相同,且都是4的倍数,然后求出第2017个图形的组数,计算即可得解.
解答 解:图①图②的直角三角形的个数相同,都是4,4=4×1,
图③图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2017图2018的直角三角形的个数相同,都是4×$\frac{2018}{2}$=4036.
故选:B.
点评 此题考查图形的变化规律,观察图形,得到变化规律:连续两个图形的直角三角形的个数相同是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
2.已知一次函数y=(m-1)x+1的图象上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1<y2,那么m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m>-1 | D. | m<-1 |
19.已知一次函数y=-x+1的图象上三个点的坐标分别是A(-2,y1),B(-1,y2),C(2,y3),则能正确反映y1、y2、y3的大小关系的是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y2>y3>y1 |
3.下列说法正确的是( )
| A. | “任意一个三角形的外角和等于180°”这一事件是不可能事件 | |
| B. | 必然事件发生的概率为0 | |
| C. | 一组数据1,6,3,9,8的极差为7 | |
| D. | “面积相等的两个三角形全等”这一事件是必然事件 |
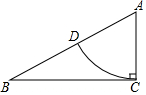 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于$\frac{π}{3}$.(结果保留π)
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于$\frac{π}{3}$.(结果保留π)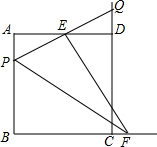 在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )
在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )