题目内容
2.已知一次函数y=(m-1)x+1的图象上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1<y2,那么m的取值范围是( )| A. | m>1 | B. | m<1 | C. | m>-1 | D. | m<-1 |
分析 先根据x1>x2时,y1<y2,得到y随x的增大而减小,所以x的比例系数小于0,那么m-1<0,解不等式即可求解.
解答 解:∵一次函数y=(m-1)x+1的图象上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1<y2,
∴y随x的增大而减小,
∴m-1<0,
∴m<1.
故选B.
点评 本题考查一次函数y=kx+b(k≠0,且k,b为常数)的图象性质:当k>0,y随x的增大而增大;当k<0时,y将随x的增大而减小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.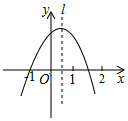 如图,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )
如图,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )
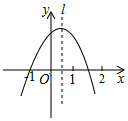 如图,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )
如图,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )| A. | ①③ | B. | ②③ | C. | ②④ | D. | ②③④ |
7. 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
步骤1:分别以点A,D为圆心,以大于$\frac{1}{2}$AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:步骤1:分别以点A,D为圆心,以大于$\frac{1}{2}$AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
| A. | 线段DE是△ABC的中位线 | B. | 四边形AFDE是菱形 | ||
| C. | MN垂直平分线段AD | D. | $\frac{BD}{DC}$=$\frac{BE}{EA}$ |
14.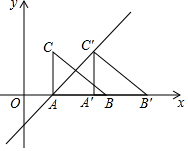 如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )
如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )
 如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )
如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )| A. | (5,3) | B. | (3,5) | C. | (6,4) | D. | (4,6) |
11.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2017个图形中直角三角形的个数有( )
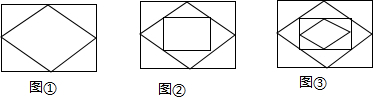

| A. | 8072个 | B. | 4036个 | C. | 4032个 | D. | 2016个 |
12.在同一直角坐标系中,若直线y=k1x与双曲线y=$\frac{{k}_{2}}{x}$没有公共点,则( )
| A. | k1k2<0 | B. | k1k2>0 | C. | k1+k2<0 | D. | k1+k2>0 |
 直线y=kx+b(k≠0)的图象如图所示,由图象可知当y<0时,x的取值范围是x<2.
直线y=kx+b(k≠0)的图象如图所示,由图象可知当y<0时,x的取值范围是x<2.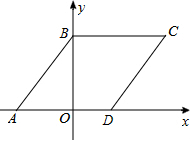 如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(-3,0),(0,4),点D在x轴正半轴上.
如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(-3,0),(0,4),点D在x轴正半轴上.