题目内容
5.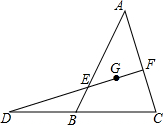 过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
分析 连接AG并延长交BC于H,作BM∥AH交DF于M,作CN∥AH交DF的延长线于N,根据重心的性质得到H是BC的中点,AG=2GH,根据梯形的中位线定理得到BM+CN=2GH,根据平行线分线段成比例定理计算即可.
解答 证明: 连接AG并延长交BC于H,作BM∥AH交DF于M,作CN∥AH交DF的延长线于N,
连接AG并延长交BC于H,作BM∥AH交DF于M,作CN∥AH交DF的延长线于N,
∵点G是△ABC的重心,
∴H是BC的中点,AG=2GH,
∴GH是梯形BCNM的中位线,即BM+CN=2GH,
∵BM∥AH,
∴$\frac{BE}{EA}$=$\frac{BM}{AG}$,
∵CN∥AH,
∴$\frac{CF}{FA}$=$\frac{CN}{AG}$,
∴$\frac{BE}{EA}$+$\frac{CF}{FA}$=$\frac{BM}{AG}$+$\frac{CN}{AG}$=$\frac{BM+CN}{AG}$=$\frac{2GH}{AG}$=1.
点评 本题考查的是三角形重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.

练习册系列答案
相关题目
15.已知抛物线y=2(x-1)2上的两点A(x1,y1)和B(x2,y2),如果x1<x2<0,那么下列结论一定成立的是( )
| A. | y1<y2<0 | B. | 0<y1<y2 | C. | 0<y2<y1 | D. | y2<y1<0 |
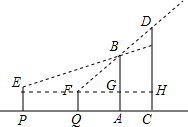 如图,两棵人树AB、CD,它们根部的距离AC=4m.小强沿着正对这两棵树的方向前进,如果小强的眼睛与地面的距离为1.6m,小强在P处时测得B的仰角为20.3°,当小强前进5m达到Q处时,视线恰好经过两棵树的顶部B和D,此时仰角为36.42°.
如图,两棵人树AB、CD,它们根部的距离AC=4m.小强沿着正对这两棵树的方向前进,如果小强的眼睛与地面的距离为1.6m,小强在P处时测得B的仰角为20.3°,当小强前进5m达到Q处时,视线恰好经过两棵树的顶部B和D,此时仰角为36.42°.
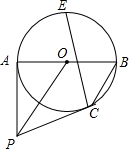 如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.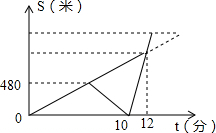 小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系.
小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系. 如图,根据图中信息解答下列问题:
如图,根据图中信息解答下列问题: 如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.
如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.