题目内容
10.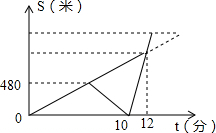 小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系.
小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系.(1)小明和哥哥离开家6分钟时,哥哥发现忘记带礼物;
(2)求出图中出租车行驶路程s与时间t的函数关系式(不必写出t的取值范围);
(3)请直接写出小明家到爷爷家的距离.
分析 (1)根据时间=路程÷速度列式计算即可得解;
(2)设出租车行驶路程s与时间t的函数关系式为s=kt+b,易知图象过点(10,0),再求出甲乙二人相遇时的坐标,然后利用待定系数法求一次函数解析式即可;
(3)设步行到达的时间为t,根据早到3分钟列出方程求出t,然后求解即可.
解答 解:(1)480÷80=6分钟.
故答案为:6;
(2)∵t=12时,s=80×12=960,
∴相遇时的点的坐标为(12,960),
设出租车行驶路程s与时间t的函数关系式为s=kt+b,
将(10,0),(12,960)代入,得$\left\{\begin{array}{l}{0=10k+b}\\{960=12k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=480}\\{b=-4800}\end{array}\right.$.
∴s与t的关系式为s=480t-4800;
(3)设步行到达的时间为t分钟,则实际到达是时间为(t-3)分钟,
由题意得,80t=480(t-3)-4800,
解得t=15.6.
所以小明家到爷爷家的距离为80×15.6=1248米.
点评 本题考查的是一次函数的应用,主要利用了路程、速度、时间三者之间的关系,待定系数法求一次函数解析式,难点在于(3)找出等量关系列出方程.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
2.一个盒子中装有2个白球、5个红球,从这个盒子中随机摸出一个球,是红球的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{2}$ |
19.下列各式中,不论字母取何值时分式都有意义的是( )
| A. | $\frac{1}{2x+1}$ | B. | $\frac{1}{2x-1}$ | C. | $\frac{1-3x}{{x}^{2}}$ | D. | $\frac{5x+3}{2{x}^{2}+1}$ |
 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.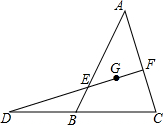 过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)