题目内容
14.如图,BC为⊙O直径,E为弧BD的中点.(1)如图1,若⊙O的半径为2,∠DCE=22.5°,过E作EG⊥BC,垂足为G,求EG的长;
(2)如图2,连接CE交BD于H,切线CA与BD的延长线交于点A,求证:AH=AC.

分析 (1)连接OE,如图1,利用圆周角定理得到∠1=∠DCE=22.5°,再利用三角形外角性质可计算出∠3=45°,则可判定△OEG为等腰直角三角形,然后根据等腰直角三角形的性质计算EG的长;
(2)连接BE,如图2,利用圆周角定理得到∠1=∠2,∠BEC=90°,则∠2+∠4=90°,再利用切线性质得∠ACB=90°,即∠1+∠ACE=90°,所以∠ACE=∠4,易得∠ACE=∠3,然后根据等腰三角形的判定定理尽快得到结论.
解答 (1)解:连接OE,如图1,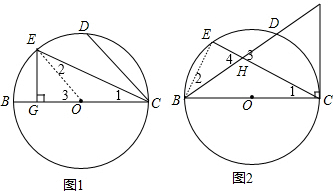
∵E为弧BD的中点,
∴∠1=∠DCE=22.5°,
∵OC=OE,
∴∠1=∠2=22.5°,
∴∠3=∠1+∠2=45°,
∵EG⊥BC,
∴△OEG为等腰直角三角形,
∴EG=$\frac{\sqrt{2}}{2}$OE=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$;
(2)证明:连接BE,如图2,
∵E为弧BD的中点,
∴∠1=∠2,
∵BC为直径,
∴∠BEC=90°,即∠2+∠4=90°,
∵AC为切线,
∴∠ACB=90°,即∠1+∠ACE=90°,
∴∠ACE=∠4,
∵∠3=∠4,
∴∠ACE=∠3,
∴AC=AH.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.解决本题的关键是灵活运用圆周角定理.

练习册系列答案
相关题目
2.一个盒子中装有2个白球、5个红球,从这个盒子中随机摸出一个球,是红球的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{2}$ |
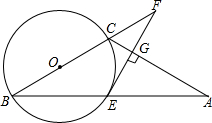 已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F. 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$. 如图,菱形ABCD中,AE平分∠BAC交BC于E,AF平分∠CAD交CD于F,求证:AE=AF.
如图,菱形ABCD中,AE平分∠BAC交BC于E,AF平分∠CAD交CD于F,求证:AE=AF.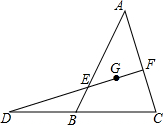 过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.