题目内容
15.已知抛物线y=2(x-1)2上的两点A(x1,y1)和B(x2,y2),如果x1<x2<0,那么下列结论一定成立的是( )| A. | y1<y2<0 | B. | 0<y1<y2 | C. | 0<y2<y1 | D. | y2<y1<0 |
分析 根据二次函数的性质得到抛物线y=2(x-1)2的开口向上,有最小值为0,对称轴为直线x=1,则在对称轴左侧,y随x的增大而减小,所以x1<x2<0时,y1>y2>0.
解答 解:∵y=2(x-1)2,
∴a=2>0,有最小值为0,
∴抛物线开口向上,
∵抛物线y=2(x-1)2对称轴为直线x=1,
∵x1<x2<0,
∴0<y2<y1.
故选C.
点评 本题考查了二次函数图象上点的坐标特征:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,则抛物线上的点的坐标满足其解析式;当a>0,抛物线开口向下;对称轴为直线x=-$\frac{b}{2a}$,在对称轴左侧,y随x的增大而减小,在对称轴右侧,y随x的增大而增大.

练习册系列答案
相关题目
6.过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为( )
| A. | 312×104 | B. | 0.312×107 | C. | 3.12×106 | D. | 3.12×107 |
7.我市5月的某一周每天的最高气温(单位:℃)统计如下:19,20,25,22,25,26,27,则这组数据的中位数与众数分别是( )
| A. | 25,25 | B. | 25,22 | C. | 20,22 | D. | 22,24 |
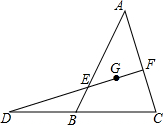 过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)