题目内容
17.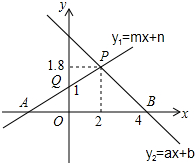 如图,根据图中信息解答下列问题:
如图,根据图中信息解答下列问题:(1)关于x的不等式ax+b>0的解集是x<4.
(2)关于x的不等式mx+n<1的解集是x<0.
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
分析 (1)利用直线y=ax+b与x轴的交点为(4,0),然后利用函数图象可得到不等式kx+b>0的解集.
(2)利用直线y=mx+n与x轴的交点为(0,1),然后利用函数图象可得到不等式mx+n<1的解集.
(3)结合两条直线的交点坐标为(2,18)来求得y1≤y2解集.
(4)结合函数图象直接写出答案.
解答  解:(1)∵直线y2=ax+b与x轴的交点是(4,0),
解:(1)∵直线y2=ax+b与x轴的交点是(4,0),
∴当x<4时,y2>0,即不等式ax+b>0的解集是x<4;
故答案是:x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时,y1<1,即不等式mx+n<1的解集是x<0;.
故答案是:x<0;
(3)由一次函数的图象知,两条直线的交点坐标是(2,18),当函数y1的图象在y2的下面时,有x≤2,
所以当x≤2时,y1≤y2;
(4)如图所示,当2<x<4时,0<y2<y1.
点评 本题考查了一次函数与一元一次不等式,解答该类题目时,需要学生具备一定的读图能力,体现了数形结合的思想方法,准确的确定出x的值,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.一个盒子中装有2个白球、5个红球,从这个盒子中随机摸出一个球,是红球的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{2}$ |
6.过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为( )
| A. | 312×104 | B. | 0.312×107 | C. | 3.12×106 | D. | 3.12×107 |
7.我市5月的某一周每天的最高气温(单位:℃)统计如下:19,20,25,22,25,26,27,则这组数据的中位数与众数分别是( )
| A. | 25,25 | B. | 25,22 | C. | 20,22 | D. | 22,24 |
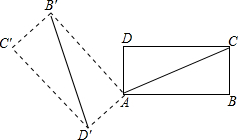 如图,在矩形ABCD中AB=3,BC=$\sqrt{3}$,若矩形ABCD绕点A逆时针旋转2∠DAC得到矩形AB′C′D′,则矩形ABCD在旋转过程中所扫过的图形的面积为4π.
如图,在矩形ABCD中AB=3,BC=$\sqrt{3}$,若矩形ABCD绕点A逆时针旋转2∠DAC得到矩形AB′C′D′,则矩形ABCD在旋转过程中所扫过的图形的面积为4π. 如图,菱形ABCD中,AE平分∠BAC交BC于E,AF平分∠CAD交CD于F,求证:AE=AF.
如图,菱形ABCD中,AE平分∠BAC交BC于E,AF平分∠CAD交CD于F,求证:AE=AF.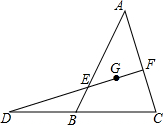 过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.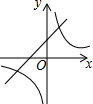 如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).
如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).