题目内容
14. 如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.
如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.
分析 由点D在AC的垂直平分线上,根据线段垂直平分线的性质,可得AD=CD,又由∠D=130°,即可求得∠DCA的度数,然后由AB∥CD,根据平行线的性质,求得∠BAC的度数.
解答 解:∵点D在AC的垂直平分线上,
∴AD=CD,
∵∠D=130°,
∴∠DAC=∠DCA=25°,
∵AB∥CD,
∴∠BAC=∠DCA=25°.
故答案为:25°.
点评 此题考查了线段垂直平分线的性质、平行线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
2.一个盒子中装有2个白球、5个红球,从这个盒子中随机摸出一个球,是红球的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{2}$ |
19.下列各式中,不论字母取何值时分式都有意义的是( )
| A. | $\frac{1}{2x+1}$ | B. | $\frac{1}{2x-1}$ | C. | $\frac{1-3x}{{x}^{2}}$ | D. | $\frac{5x+3}{2{x}^{2}+1}$ |
6.过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为( )
| A. | 312×104 | B. | 0.312×107 | C. | 3.12×106 | D. | 3.12×107 |
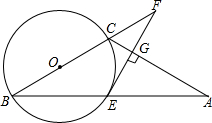 已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.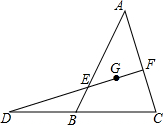 过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.
过△ABC的重心G的直线分别交AB、AC于点E、F,交CB的延长线于点D,求证:$\frac{BE}{EA}$+$\frac{CF}{FA}$=1.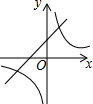 如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).
如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).