题目内容
某科技小组制作了一个机器人,它能根据指令要求进行行进和旋转,某一指令规定:机器人先向前方行走2 m,然后左转60°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了多少米?
 机器人共走了12 m.
【解析】分析:第一次回到原处正好转了360°,正好构成一个正六边形,先理解题目意思,再去看关键字来思考问题,来解决问题,最终得出答案.
本题解析:
机器人转了一周共360度,360°÷60°=6,共走了6次,机器人走了6×2=12米.
故答案为:12米.
机器人共走了12 m.
【解析】分析:第一次回到原处正好转了360°,正好构成一个正六边形,先理解题目意思,再去看关键字来思考问题,来解决问题,最终得出答案.
本题解析:
机器人转了一周共360度,360°÷60°=6,共走了6次,机器人走了6×2=12米.
故答案为:12米.
练习册系列答案
相关题目
下列结论中,正确的是( )
A. 若a>b,则 <
<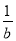 B. 若a>b,则a2>b2
B. 若a>b,则a2>b2
C. 若a>b,则1-a<1-b D. 若a>b,ac2>bc2
 C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C.
C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C. 不能判断四边形ABCD是平行四边形的是( )
A. AB=CD,AD=BC B. AB=CD,AB∥CD
C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
 C
【解析】平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断,
平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴B能判断;
平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴D能判定;
平行四边形判定定理3,对角线互相平分的四边形是平行四边形;
平行四边形判定定理4,一组对边平行相等的四边形是平行四边形;
故选A.
...
C
【解析】平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断,
平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴B能判断;
平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴D能判定;
平行四边形判定定理3,对角线互相平分的四边形是平行四边形;
平行四边形判定定理4,一组对边平行相等的四边形是平行四边形;
故选A.
... 若不等式(a-2)x>a-2可以变形为x<1,则a的取值范围为_____.
 a<2
【解析】根据一元一次不等式的解法和基本性质,可由(a-2)x>a-2的解集为x<1,可知a-2<0,解得a<2.
故答案为:a<2.
a<2
【解析】根据一元一次不等式的解法和基本性质,可由(a-2)x>a-2的解集为x<1,可知a-2<0,解得a<2.
故答案为:a<2. 下列各项中,不是不等式x≤2解的是( )
A. 0 B. 2 C. 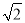 D.
D. 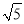
 D
【解析】由于>2,所以不是x≤2的解.
故选:D.
D
【解析】由于>2,所以不是x≤2的解.
故选:D. 已知多边形内角和与外角和的和为2160°,求多边形对角线的条数.
 54
【解析】分析:已知一个多边形的内角和与外角和的差为2160°,外角和是360度,因而内角和是1800度.n边形的内角和是(n-2) ×180°,代入就得到一个关于n的方程,就可以解得边数n,从而得到这个多边形的对角线的条数.
本题解析:
设这是n边形,则
(n-2)×180°=2160°-360°,
n-2=10,
n=12.
这个多边形的对角线的条数=12×(12...
54
【解析】分析:已知一个多边形的内角和与外角和的差为2160°,外角和是360度,因而内角和是1800度.n边形的内角和是(n-2) ×180°,代入就得到一个关于n的方程,就可以解得边数n,从而得到这个多边形的对角线的条数.
本题解析:
设这是n边形,则
(n-2)×180°=2160°-360°,
n-2=10,
n=12.
这个多边形的对角线的条数=12×(12... 若一个三角形的三边长分别为3 m,4 m,5 m,那么这个三角形的面积为___.
 6 m2
【解析】根据勾股定理的逆定理,可由三边的长判断出此三角形是直角三角形,3cm、4cm是三角形的两直角边,所以根据三角形的面积公式可得面积为3×4÷2=6m2.
故答案为:6m2.
6 m2
【解析】根据勾股定理的逆定理,可由三边的长判断出此三角形是直角三角形,3cm、4cm是三角形的两直角边,所以根据三角形的面积公式可得面积为3×4÷2=6m2.
故答案为:6m2. 化简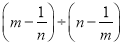 的结果是( )
的结果是( )
A. 1 B. 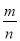 C.
C. 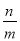 D. -1
D. -1
 B
【解析】试题分析:
=
=
=.
故选B.
B
【解析】试题分析:
=
=
=.
故选B. 如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_______°.

 【解析】∵□ABCD与□DCFE的周长相等,且有公共边CD,
∴AD=DE,∠ADE=∠BCF=60°+70°=130°.
∴.
【解析】∵□ABCD与□DCFE的周长相等,且有公共边CD,
∴AD=DE,∠ADE=∠BCF=60°+70°=130°.
∴. 
