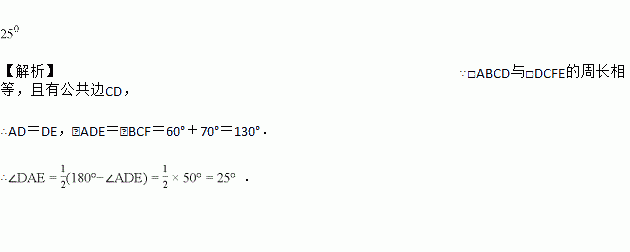题目内容
如图，□ABCD与□DCFE的周长相等，且∠BAD=60°，∠F=110°，则∠DAE的度数为_______°．
【解析】∵□ABCD与□DCFE的周长相等，且有公共边CD，
∴AD＝DE，∠ADE＝∠BCF＝60°＋70°＝130°．
∴．
某科技小组制作了一个机器人，它能根据指令要求进行行进和旋转，某一指令规定：机器人先向前方行走2 m，然后左转60°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了多少米?
机器人共走了12 m.
【解析】分析：第一次回到原处正好转了360°，正好构成一个正六边形，先理解题目意思，再去看关键字来思考问题，来解决问题，最终得出答案．
本题解析：
机器人转了一周共360度，360°÷60°=6，共走了6次，机器人走了6×2=12米．
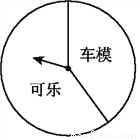
故答案为：12米． 某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
（1）472，0.596；（2）0.6，0.6；（3）144°.
【解析】试题分析: 在同样条件下,做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率,
（1）当试验的可能结果不是有限个,或各种结果发生的可能性不相等时,一般用统计频率的方法来估计概率,
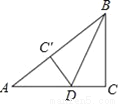
（2）利用频率估计概率的数学依据是大数定律:当试验次数很大时,随机事件A出现的频率,稳定... 如图，在Rt△ABC中，∠C=90°，BC=6cm，AC=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是__．
6cm2
【解析】试题分析：先根据勾股定理得到AB=10cm，再根据折叠的性质得到DC=DC′，BC=BC′=6cm，则AC′=4cm，设DC=xcm，在Rt△ADC′中根据勾股定理列方程求得x的值，然后根据三角形的面积公式计算即可．
∵∠C=90°，BC=6cm，AC=8cm，
∴AB=10cm，
∵将△BCD沿BD折叠，使点C落在AB边的C′点，
∴△BCD≌△B... 在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．
（1）如图①，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
（2）如图②，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．
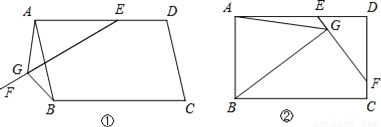
（1）证明见解析；（2）EG=AG﹣BG，理由见解析．
【解析】试题分析：（1）如图，作∠GAH=∠EAB交GE于点H，易证△ABG≌△AEH ，再判定△AGH是等边三角形，即可得结论；（2）EG=AG-BG，如图②，作∠GAH=∠EAB交GE于点H，类比（1）的方法证明△ABG≌△AEH，再判定△AGH是等腰直角三角形，即可得结论.
试题解析：
如图，作∠GAH=∠EAB交GE... 如图，在平行四边形ABCD中，AB＞BC，按以下步骤作图：以A为圆心，小于AD的长为半径画弧，分别交AB、CD于E、F；再分别以E、F为圆心，大于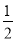
EF的长半径画弧，两弧交于点G；作射线AG交CD于点H．则下列结论：①AG平分∠DAB，②CH=
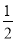DH，③△ADH是等腰三角形，④S△ADH=
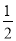S四边形ABCH．
其中正确的有（ ）
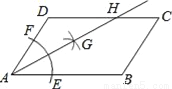
A. ①②③ B. ①③④ C. ②④ D. ①③
D
【解析】试题分析：①如图，连接EG，FG，
由作图可得，AE=AF，EG=FG，
又∵AG=AG，∴△AEG≌△AFG（SSS）。
∴∠EAG=∠FAG，即AG平分∠DAB。故结论①正确。
③∵在平行四边形ABCD中，DC∥AB，∴∠HAB=DHA。
由①∠HAB=∠HAD，∴∠HAD=DHA。∴DA=DH，即△ADH是等腰三角形。故结论③正确。
②若... 掷一枚正方体的骰子，各个面上分别标有数字1， 2，3，4，5，6，求下列事件发生的频率的大小：
①朝上的数字是奇数；
②朝上的数字能被3除余1；
③朝上的数字不是3的倍数；
④朝上的数字小于6；
⑤朝上的数字不小于3.
①；②；③；④；⑤
【解析】试题分析:本题考察可能性大小的应用，关键是推断出各色扑克被抽到的频率是多少.
①【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，每一个点数出现的频率相同.其中，是奇数点的有3种可能，故其频率是；
②【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，... 下列说法正确的是( )
A. 如果一件事情发生的可能性达到99.9999%，说明这件事必然发生；
B. 如果一事件不是不可能事件,说明此事件是不确定事件；
C. 可能性的大小与不确定事件有关；
D. 如果一事件发生的可能性为百万分之一，那么这事件是不可能事件.
C
【解析】试题分析：根据必然事件、不可能事件、不确定事件的概念依次分析即可.
A.如果一件事情发生的可能性达到99.9999%,说明这件事很可能发生，但仍然是不确定事件，故错误；
B.如果一事件不是不可能事件,说明此事件是不确定事件或必然事件，故错误；
C.可能性的大小与不确定事件有关，正确；
D.如果一事件发生的可能性为百万分之一，这事件是不确定事件，故错误；
... 正方形既是_________图形，又是_____________图形
轴对称 中心对称
【解析】正方形既是轴对称图形又是中心对称图形.
故答案：轴对称，中心对称.