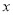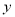题目内容
下列结论中，正确的是( )
A. 若a＞b，则
＜
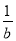B. 若a＞b，则a2＞b2
C. 若a＞b，则1－a＜1－b D. 若a＞b，ac2＞bc2
C
【解析】当1＞a＞b＞0时， ＜，故不正确；当a＞0，b＜0，a＜|b|时，a2＜b2，故不正确；由a＞b可知-a＜-b，因此可得1-a＜1-b，故正确；当c=0时，虽然a＞b，但是ac2=bc2=0，故不正确.
故选：C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在一块边长为a的正方形纸板四周，各剪去一个边长为b(b＜0)的正方形．
(1)用代数式表示阴影部分的面积；
(2)利用因式分解的方法计算当a＝15.4，b＝3.7时，阴影部分的面积．
(1) a2－4b²;(2) 182.4.
【解析】试题分析：
试题解析：（1）用大正方形的面积减去四个小正方形的面积即可求得阴影部分的面积；（2）把所得的代数式用平方差公式因式分解后，代入求值即可.
(1)S阴影＝a2－4b2；
(2)S阴影＝(a＋2b)(a－2b)＝(15.4＋2×3.7)(15.4－2×3.7)＝22.8×8＝182.4. 二次函数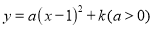
中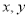
的几组对应值如下表．
| -2 | 1 | 5 |
| m | n | p |
表中m、n、p的大小关系为________________（用“＜”连接）
n＜m＜p
【解析】【解析】
设（-2，m）关于对称轴的对称点为（x，m）．∵二次函数的对称轴为x=1，∴ ，解得：x=4．∵a＞0，∴抛物线开口向上，在对称轴右侧，y随x的增大而增大．∵1＜4＜5，∴n＜m＜p．故答案为：n＜m＜p． 课外阅读课上，老师将43本书分给各小组，每组8本，还有剩余；每组9本却又不够，问有几个小组？
x＝5.
【解析】试题分析：根据题意中的不等关系，设有x个小组，列不等式组求解，然后判断出正整数解即可.
试题解析：设有x个小组，题意得，解得：＜x＜，因为x为正整数，所以x＝5. 不等式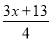
＞
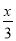＋2的解是_________.
x＞－3
【解析】＞＋2, 去分母得： 去括号得： 移项及合并得： 系数化为1得： .
故答案为x＞－3. 如图所示，在四边形ABCD中，已知AB与 CD不平行，∠ABD＝∠ACD，请你添加一个条件：______ ，使的加上这个条件后能够推出AD∥BC ，且AB＝CD．
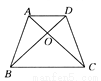
∠DAC＝∠ADB或∠BAD＝∠CDA或∠DBC＝∠ACB或∠ABC＝∠DCB或OB＝OC或OA＝OD.
【解析】试题分析：先证四边形AECO是梯形，再说明是等腰梯形．由题意可知，∠ABD=∠ACD，AD是△BAD和△CDA的公共边，则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA，同理可添加∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD，从而推出AD∥BC且AB=C... 在□ABCD中，AB=3，BC=4，则□ABCD的周长等于_______.
14
【解析】【解析】
∵四边形ABCD是平行四边形，∴CD=AB=3，AD=BC=4，∴?ABCD的周长为14．
故答案为：14． 已知某个平行四边形的一边长为7，一条对角线长为8，求另一条对角线长的取值范围．
6＜x＜22．
【解析】试题分析：由平行四边形的对角线互相平分，根据三角形三边之间的关系，可先求得另一对角线的一半的取值范围，进而可求出这条对角线的范围．
试题解析：【解析】
如图，已知平行四边形中，AB=7，AC=8．由题意得，BD=2OB，AC=2OA=8，∴OB=BD，OA=4．在△AOB中，AB﹣OA＜OB＜AB+OA，可得3＜OB＜11，即6＜BD＜22．故答案为：6＜BD... 某科技小组制作了一个机器人，它能根据指令要求进行行进和旋转，某一指令规定：机器人先向前方行走2 m，然后左转60°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了多少米?
机器人共走了12 m.
【解析】分析：第一次回到原处正好转了360°，正好构成一个正六边形，先理解题目意思，再去看关键字来思考问题，来解决问题，最终得出答案．
本题解析：
机器人转了一周共360度，360°÷60°=6，共走了6次，机器人走了6×2=12米．
故答案为：12米．