题目内容
已知多边形内角和与外角和的和为2160°，求多边形对角线的条数．
54
【解析】分析：已知一个多边形的内角和与外角和的差为2160°,外角和是360度,因而内角和是1800度.n边形的内角和是(n-2) ×180°,代入就得到一个关于n的方程,就可以解得边数n,从而得到这个多边形的对角线的条数.
本题解析：
设这是n边形,则
（n-2）×180°=2160°-360°,
n-2=10,
n=12.
这个多边形的对角线的条数=12×(12...
如图所示，在四边形ABCD中，已知AB与 CD不平行，∠ABD＝∠ACD，请你添加一个条件：______ ，使的加上这个条件后能够推出AD∥BC ，且AB＝CD．
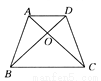
∠DAC＝∠ADB或∠BAD＝∠CDA或∠DBC＝∠ACB或∠ABC＝∠DCB或OB＝OC或OA＝OD.
【解析】试题分析：先证四边形AECO是梯形，再说明是等腰梯形．由题意可知，∠ABD=∠ACD，AD是△BAD和△CDA的公共边，则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA，同理可添加∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD，从而推出AD∥BC且AB=C... 辽宁南部素以“苹果之乡”著称，某乡组织10辆汽车装运A、B两种苹果到外地销售，按规定每辆汽车只装同一种苹果，且必须装满．已知A、B两种苹果的每辆车运载量及每吨苹果获利如下表：
苹果品种 | A | B |
每辆汽车运载量(吨) | 3 | 2 |
每吨苹果获利(百元) | 5 | 9 |
(1)要求共运出苹果至少24吨，试写出装运A种苹果的汽车x(辆)应满足的不等式；
(2)要求共获利不少于15600元，试写出装运A种苹果汽车x(辆)应满足的另一个不等式．
(1) 3x＋2(10－x)≥24； (2) 【解析】
1500x＋1800(10－x)≥15600
【解析】试题分析：（1）设x辆汽车运A种苹果，则有（10-x）辆汽车运B种苹果，根据题意可得不等关系：运出苹果超过24吨；②一次性获利超过15600元，根据不等关系列出不等式组；
（2）设x辆汽车运A种苹果，则有（10-x）辆汽车运B种苹果，根据题意可得不等关系：一次性获利超过15600... 函数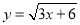
中自变量x的取值范围在数轴上表示正确的是（ ）
A．
B．
C．
D．
A．
【解析】
试题分析：由函数，得到3x+6≥0，解得：x≥﹣2，表示在数轴上，如图所示：
故选A． 某科技小组制作了一个机器人，它能根据指令要求进行行进和旋转，某一指令规定：机器人先向前方行走2 m，然后左转60°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了多少米?
机器人共走了12 m.
【解析】分析：第一次回到原处正好转了360°，正好构成一个正六边形，先理解题目意思，再去看关键字来思考问题，来解决问题，最终得出答案．
本题解析：
机器人转了一周共360度，360°÷60°=6，共走了6次，机器人走了6×2=12米．
故答案为：12米． 如图，在△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB，交BC于点D，若CD＝1，则BD＝________．
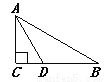
2
【解析】试题分析：根据角平分线性质求出∠BAD的度数，根据含30度角的直角三角形性质求出AD即可得BD．
∵∠C=90°，∠B=30°，∴∠CAB=60°，AD平分∠CAB，∴∠BAD=30°，∴BD=AD=2CD=2， 如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB．若BE=2，则AE的长为（ ）
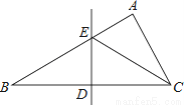
A.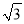 
B. 1 C. 
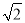D. 2
B
【解析】试题解析：∵在△ABC中，∠B=30°，BC的垂直平分线交AB于E，BE=2，
∴BE=CE=2，
∴∠B=∠DCE=30°，
∵CE平分∠ACB，
∴∠ACB=2∠DCE=60°，∠ACE=∠DCE=30°，
∴∠A=180°-∠B-∠ACB=90°．
在Rt△CAE中，∵∠A=90°，∠ACE=30°，CE=2，
∴AE=CE=1．
... 若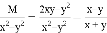
,则M=___________.
【解析】本题考查的是等式的性质
①将等号右边通分,得,比较等号左边的分式,不难得出. ②可以在等号两边都乘以后，化简右边即可.
①将等号右边通分，得，故；
②等号两边都乘得 如图，在平行四边形ABCD中，AB＞BC，按以下步骤作图：以A为圆心，小于AD的长为半径画弧，分别交AB、CD于E、F；再分别以E、F为圆心，大于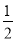
EF的长半径画弧，两弧交于点G；作射线AG交CD于点H．则下列结论：①AG平分∠DAB，②CH=
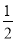DH，③△ADH是等腰三角形，④S△ADH=
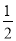S四边形ABCH．
其中正确的有（ ）
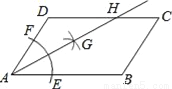
A. ①②③ B. ①③④ C. ②④ D. ①③
D
【解析】试题分析：①如图，连接EG，FG，
由作图可得，AE=AF，EG=FG，
又∵AG=AG，∴△AEG≌△AFG（SSS）。
∴∠EAG=∠FAG，即AG平分∠DAB。故结论①正确。
③∵在平行四边形ABCD中，DC∥AB，∴∠HAB=DHA。
由①∠HAB=∠HAD，∴∠HAD=DHA。∴DA=DH，即△ADH是等腰三角形。故结论③正确。
②若...