题目内容
若不等式(a－2)x＞a－2可以变形为x＜1，则a的取值范围为_____.
a＜2
【解析】根据一元一次不等式的解法和基本性质，可由(a－2)x＞a－2的解集为x＜1，可知a-2＜0，解得a＜2.
故答案为：a＜2.
练习册系列答案
相关题目
课外阅读课上，老师将43本书分给各小组，每组8本，还有剩余；每组9本却又不够，问有几个小组？
x＝5.
【解析】试题分析：根据题意中的不等关系，设有x个小组，列不等式组求解，然后判断出正整数解即可.
试题解析：设有x个小组，题意得，解得：＜x＜，因为x为正整数，所以x＝5. 已知某个平行四边形的一边长为7，一条对角线长为8，求另一条对角线长的取值范围．
6＜x＜22．
【解析】试题分析：由平行四边形的对角线互相平分，根据三角形三边之间的关系，可先求得另一对角线的一半的取值范围，进而可求出这条对角线的范围．
试题解析：【解析】
如图，已知平行四边形中，AB=7，AC=8．由题意得，BD=2OB，AC=2OA=8，∴OB=BD，OA=4．在△AOB中，AB﹣OA＜OB＜AB+OA，可得3＜OB＜11，即6＜BD＜22．故答案为：6＜BD... 辽宁南部素以“苹果之乡”著称，某乡组织10辆汽车装运A、B两种苹果到外地销售，按规定每辆汽车只装同一种苹果，且必须装满．已知A、B两种苹果的每辆车运载量及每吨苹果获利如下表：
苹果品种 | A | B |
每辆汽车运载量(吨) | 3 | 2 |
每吨苹果获利(百元) | 5 | 9 |
(1)要求共运出苹果至少24吨，试写出装运A种苹果的汽车x(辆)应满足的不等式；
(2)要求共获利不少于15600元，试写出装运A种苹果汽车x(辆)应满足的另一个不等式．
(1) 3x＋2(10－x)≥24； (2) 【解析】
1500x＋1800(10－x)≥15600
【解析】试题分析：（1）设x辆汽车运A种苹果，则有（10-x）辆汽车运B种苹果，根据题意可得不等关系：运出苹果超过24吨；②一次性获利超过15600元，根据不等关系列出不等式组；
（2）设x辆汽车运A种苹果，则有（10-x）辆汽车运B种苹果，根据题意可得不等关系：一次性获利超过15600... 不等式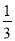
(x－m)＞3－m的解集为x＞1，则m的值为___.
x＞6
【解析】试题分析：去分母得，x﹣m＞3（3﹣m），
去括号得，x﹣m＞9﹣3m，
移项，合并同类项得，x＞9﹣2m。
∵此不等式的解集为x＞1，
∴9﹣2m=1，解得m=4。 函数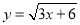
中自变量x的取值范围在数轴上表示正确的是（ ）
A．
B．
C．
D．
A．
【解析】
试题分析：由函数，得到3x+6≥0，解得：x≥﹣2，表示在数轴上，如图所示：
故选A． 某科技小组制作了一个机器人，它能根据指令要求进行行进和旋转，某一指令规定：机器人先向前方行走2 m，然后左转60°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了多少米?
机器人共走了12 m.
【解析】分析：第一次回到原处正好转了360°，正好构成一个正六边形，先理解题目意思，再去看关键字来思考问题，来解决问题，最终得出答案．
本题解析：
机器人转了一周共360度，360°÷60°=6，共走了6次，机器人走了6×2=12米．
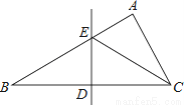
故答案为：12米． 如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB．若BE=2，则AE的长为（ ）
A.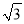 
B. 1 C. 
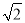D. 2
B
【解析】试题解析：∵在△ABC中，∠B=30°，BC的垂直平分线交AB于E，BE=2，
∴BE=CE=2，
∴∠B=∠DCE=30°，
∵CE平分∠ACB，
∴∠ACB=2∠DCE=60°，∠ACE=∠DCE=30°，
∴∠A=180°-∠B-∠ACB=90°．
在Rt△CAE中，∵∠A=90°，∠ACE=30°，CE=2，
∴AE=CE=1．
... 如图，在Rt△ABC中，∠C=90°，BC=6cm，AC=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是__．
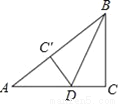
6cm2
【解析】试题分析：先根据勾股定理得到AB=10cm，再根据折叠的性质得到DC=DC′，BC=BC′=6cm，则AC′=4cm，设DC=xcm，在Rt△ADC′中根据勾股定理列方程求得x的值，然后根据三角形的面积公式计算即可．
∵∠C=90°，BC=6cm，AC=8cm，
∴AB=10cm，
∵将△BCD沿BD折叠，使点C落在AB边的C′点，
∴△BCD≌△B...