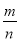��Ŀ����
�����ж��ı���ABCD��ƽ���ı��ε��ǣ� ��
A. AB=CD��AD=BC B. AB=CD��AB��CD
C. AB=CD��AD��BC D. AB��CD��AD��BC
 C
��������ƽ���ı��εĶ��壺����Ա߷ֱ�ƽ�е��ı��ν���ƽ���ı��Σ���C���жϣ�
ƽ���ı����ж�����1������ԽǷֱ���ȵ��ı�����ƽ���ı��Σ���B���жϣ�
ƽ���ı����ж�����2������Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ���D���ж���
ƽ���ı����ж�����3���Խ�����ƽ�ֵ��ı�����ƽ���ı��Σ�
ƽ���ı����ж�����4��һ��Ա�ƽ����ȵ��ı�����ƽ���ı��Σ�
��ѡA��
...
C
��������ƽ���ı��εĶ��壺����Ա߷ֱ�ƽ�е��ı��ν���ƽ���ı��Σ���C���жϣ�
ƽ���ı����ж�����1������ԽǷֱ���ȵ��ı�����ƽ���ı��Σ���B���жϣ�
ƽ���ı����ж�����2������Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ���D���ж���
ƽ���ı����ж�����3���Խ�����ƽ�ֵ��ı�����ƽ���ı��Σ�
ƽ���ı����ж�����4��һ��Ա�ƽ����ȵ��ı�����ƽ���ı��Σ�
��ѡA��
...
�����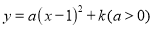 ��
��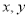 �ļ����Ӧֵ���±���
�ļ����Ӧֵ���±���
| -2 | 1 | 5 |
| m | n | p |
����m��n��p�Ĵ�С��ϵΪ________________���á��������ӣ�
 n��m��p
����������������
�裨-2��m�����ڶԳ���ĶԳƵ�Ϊ��x��m�����߶��κ����ĶԳ���Ϊx=1���� ����ã�x=4����a��0���������߿������ϣ��ڶԳ����Ҳ࣬y��x�����������1��4��5����n��m��p���ʴ�Ϊ��n��m��p��
n��m��p
����������������
�裨-2��m�����ڶԳ���ĶԳƵ�Ϊ��x��m�����߶��κ����ĶԳ���Ϊx=1���� ����ã�x=4����a��0���������߿������ϣ��ڶԳ����Ҳ࣬y��x�����������1��4��5����n��m��p���ʴ�Ϊ��n��m��p�� �ڡ�ABCD�У�AB=3��BC=4�����ABCD���ܳ�����_______.
 14
����������������
���ı���ABCD��ƽ���ı��Σ���CD=AB=3��AD=BC=4����?ABCD���ܳ�Ϊ14��
�ʴ�Ϊ��14��
14
����������������
���ı���ABCD��ƽ���ı��Σ���CD=AB=3��AD=BC=4����?ABCD���ܳ�Ϊ14��
�ʴ�Ϊ��14�� ��֪ij��ƽ���ı��ε�һ�߳�Ϊ7��һ���Խ��߳�Ϊ8������һ���Խ��߳���ȡֵ��Χ��
 6��x��22��
�������������������ƽ���ı��εĶԽ�����ƽ�֣���������������֮��Ĺ�ϵ�����������һ�Խ��ߵ�һ���ȡֵ��Χ����������������Խ��ߵķ�Χ��
�����������������
��ͼ����֪ƽ���ı����У�AB=7��AC=8��������ã�BD=2OB��AC=2OA=8����OB=BD��OA=4���ڡ�AOB�У�AB��OA��OB��AB+OA���ɵ�3��OB��11����6��BD��22���ʴ�Ϊ��6��BD...
6��x��22��
�������������������ƽ���ı��εĶԽ�����ƽ�֣���������������֮��Ĺ�ϵ�����������һ�Խ��ߵ�һ���ȡֵ��Χ����������������Խ��ߵķ�Χ��
�����������������
��ͼ����֪ƽ���ı����У�AB=7��AC=8��������ã�BD=2OB��AC=2OA=8����OB=BD��OA=4���ڡ�AOB�У�AB��OA��OB��AB+OA���ɵ�3��OB��11����6��BD��22���ʴ�Ϊ��6��BD... �ı���ABCD�У�AD//BC��AD��BC�����ı���ABCD��_______�ı��Σ�
 ƽ��
����������������
��AD//BC��AD��BC�����ı���ABCD��ƽ���ı��Σ��ʴ�Ϊ��ƽ�У�
ƽ��
����������������
��AD//BC��AD��BC�����ı���ABCD��ƽ���ı��Σ��ʴ�Ϊ��ƽ�У� �����ϲ����ԡ�ƻ��֮�硱���ƣ�ij����֯10������װ��A��B����ƻ����������ۣ����涨ÿ������ֻװͬһ��ƻ�����ұ���װ������֪A��B����ƻ����ÿ������������ÿ��ƻ���������±���
ƻ��Ʒ�� | A | B |
ÿ������������(��) | 3 | 2 |
ÿ��ƻ������(��Ԫ) | 5 | 9 |
(1)Ҫ���˳�ƻ������24�֣���д��װ��A��ƻ��������x(��)Ӧ����IJ���ʽ��
(2)Ҫ����������15600Ԫ����д��װ��A��ƻ������x(��)Ӧ�������һ������ʽ��
 (1) 3x��2(10��x)��24�� (2) ��������
1500x��1800(10��x)��15600
�������������������1����x��������A��ƻ�������У�10-x����������B��ƻ������������ɵò��ȹ�ϵ���˳�ƻ������24�֣���һ���Ի�������15600Ԫ�����ݲ��ȹ�ϵ�г�����ʽ�飻
��2����x��������A��ƻ�������У�10-x����������B��ƻ������������ɵò��ȹ�ϵ��һ���Ի�������15600...
(1) 3x��2(10��x)��24�� (2) ��������
1500x��1800(10��x)��15600
�������������������1����x��������A��ƻ�������У�10-x����������B��ƻ������������ɵò��ȹ�ϵ���˳�ƻ������24�֣���һ���Ի�������15600Ԫ�����ݲ��ȹ�ϵ�г�����ʽ�飻
��2����x��������A��ƻ�������У�10-x����������B��ƻ������������ɵò��ȹ�ϵ��һ���Ի�������15600... ����ʽ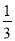 (x��m)��3��m�Ľ⼯Ϊx��1����m��ֵΪ___.
(x��m)��3��m�Ľ⼯Ϊx��1����m��ֵΪ___.
 x��6
�����������������ȥ��ĸ�ã�x��m��3��3��m����
ȥ���ŵã�x��m��9��3m��
����ϲ�ͬ����ã�x��9��2m��
�ߴ˲���ʽ�Ľ⼯Ϊx��1��
��9��2m=1�����m=4��
x��6
�����������������ȥ��ĸ�ã�x��m��3��3��m����
ȥ���ŵã�x��m��9��3m��
����ϲ�ͬ����ã�x��9��2m��
�ߴ˲���ʽ�Ľ⼯Ϊx��1��
��9��2m=1�����m=4�� ij�Ƽ�С��������һ�������ˣ����ܸ���ָ��Ҫ������н�����ת��ijһָ��涨������������ǰ������2 m��Ȼ����ת60�㣬�������˷���ִ����һָ���ӳ�������һ�λص�ԭ���������˹����˶�����?
 �����˹�����12 m.
����������������һ�λص�ԭ������ת��360�㣬���ù���һ���������Σ���������Ŀ��˼����ȥ���ؼ�����˼�����⣬��������⣬���յó��𰸣�
���������
������ת��һ�ܹ�360�ȣ�360���60��=6��������6�Σ�����������6��2=12�ף�
�ʴ�Ϊ��12�ף�
�����˹�����12 m.
����������������һ�λص�ԭ������ת��360�㣬���ù���һ���������Σ���������Ŀ��˼����ȥ���ؼ�����˼�����⣬��������⣬���յó��𰸣�
���������
������ת��һ�ܹ�360�ȣ�360���60��=6��������6�Σ�����������6��2=12�ף�
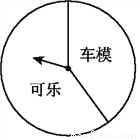
�ʴ�Ϊ��12�ף� ij�̳�����һ���ڼ����һ���н����۵Ļ,������һ����������ת����ת��(��ͼ),���涨:�˿���100Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ���,��ת��ֹͣʱ,ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ(��ָ��������������Ľ��紦,������ת��ת��).�±��Ǵ˴δ�����е�һ��ͳ������:
ת��ת�̵Ĵ���n | 100 | 200 | 400 | 500 | 800 | 1 000 |
���ڡ����֡����� �Ĵ���m | 60 | 122 | 240 | 298 | 604 | |
���ڡ����֡� �����Ƶ�� | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)���㲢�����������;
(2)����Ƶ�n�ܴ�ʱ,Ƶ�ʽ���ӽ�__________;������ȥת����ת��һ��,���á����֡��ĸ���Լ��__________;(�����ȷ��0.1)
(3)�ڸ�ת����,��ʾ����ģ����������ε�Բ�Ľ�Լ�Ƕ��ٶ�?
 ��1��472��0.596����2��0.6��0.6����3��144��.
���������������: ��ͬ��������,���������ظ����飬����һ������¼�������Ƶ�����ȶ���ij������,���Թ�������¼������ĸ���,
��1��������Ŀ��ܽ����������,����ֽ�������Ŀ����Բ����ʱ,һ����ͳ��Ƶ�ʵķ��������Ƹ���,
��2������Ƶ�ʹ��Ƹ��ʵ���ѧ�����Ǵ�������:����������ܴ�ʱ,����¼�A���ֵ�Ƶ��,�ȶ�...
��1��472��0.596����2��0.6��0.6����3��144��.
���������������: ��ͬ��������,���������ظ����飬����һ������¼�������Ƶ�����ȶ���ij������,���Թ�������¼������ĸ���,
��1��������Ŀ��ܽ����������,����ֽ�������Ŀ����Բ����ʱ,һ����ͳ��Ƶ�ʵķ��������Ƹ���,
��2������Ƶ�ʹ��Ƹ��ʵ���ѧ�����Ǵ�������:����������ܴ�ʱ,����¼�A���ֵ�Ƶ��,�ȶ�...