题目内容
8.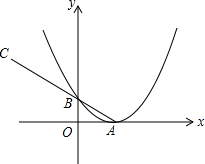 如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.
如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.
分析 先求出A点和B点坐标作CH⊥x轴于H点,如图,再利用平行线分线段成比例定理求出AH和CH的长,从而得到C点坐标,抛物线y=$\frac{1}{4}$(x-2)2向左平移n个单位所的抛物线解析式为y=$\frac{1}{4}$(x-2+n)2,由于抛物线y=$\frac{1}{4}$(x-2-n)2第一次经过点C之前,抛物线与线段AC总有两个交点,所以把C点坐标代入y=$\frac{1}{4}$(-4-2+n)2得n的最大值,从而可确定n的范围.
解答 解:y=$\frac{1}{4}$x2-x+1=$\frac{1}{4}$(x-2)2,则A(2,0),B(0,1),
作CH⊥x轴于H点,如图,
∵OB∥CH,
∴$\frac{OB}{CH}$=$\frac{OA}{AH}$=$\frac{AB}{AC}$=$\frac{1}{3}$,
∴CH=3,AH=6,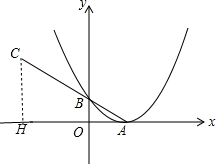
∴C(-4,3),
∵抛物线y=$\frac{1}{4}$(x-2)2向左平移n个单位所的抛物线解析式为y=$\frac{1}{4}$(x-2+n)2,
当抛物线y=$\frac{1}{4}$(x-2-n)2第一次经过点C时,$\frac{1}{4}$(-4-2+n)2=3,解得n=6+2$\sqrt{3}$(舍去)或n=6-2$\sqrt{3}$,
∴当平移后的抛物线与线段AC总有两个交点时,n的范围为0≤n≤6-2$\sqrt{3}$.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.解决本题的关键是求出C点坐标.

 名校课堂系列答案
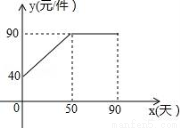
名校课堂系列答案(本小题满分8分) 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设
该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w
(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
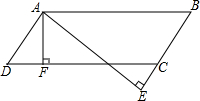 如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.
如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.
 如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°.
如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°. 如图,在周长为40cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为20cm.
如图,在周长为40cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为20cm.