题目内容
17. 如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°.
如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°.
分析 由平行四边形的性质得出∠AEB=∠CBE,由角平分线的定义和邻补角关系得出∠ABE=∠CBE=∠AEB=180°-∠BED=30°,再由三角形内角和定理即可得出∠A的度数.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵∠ABC的平分线交AD于E,∠BED=150°,
∴∠ABE=∠CBE=∠AEB=180°-∠BED=30°,
∴∠A=180°-∠ABE-∠AEB=120°;
故答案为:120°.
点评 本题考查了平行四边形的性质、三角形内角和定理;熟练掌握平行四边形的性质,求出∠ABE=∠CBE=∠AEB是解决问题的关键.

练习册系列答案
相关题目
12.多项式5mx3+25mx2-10mxy各项的公因式是( )
| A. | 5mx2 | B. | 5mxy | C. | mx | D. | 5mx |
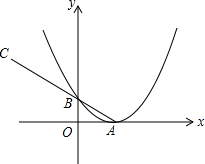 如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.
如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.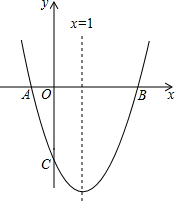 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点.交y轴与C点,已知抛物线的对称轴为x=1,B(3,0),C(0,-3)
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点.交y轴与C点,已知抛物线的对称轴为x=1,B(3,0),C(0,-3)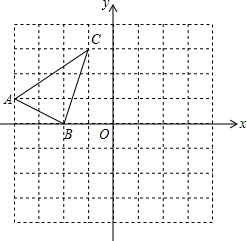 (1)请你把△ABC平移到△DEF,使点A(-4,1)的对应点D的坐标为(1,-2),B、C的对应点分别为E、F.
(1)请你把△ABC平移到△DEF,使点A(-4,1)的对应点D的坐标为(1,-2),B、C的对应点分别为E、F. 如图,将三角形ABC沿BC方向平移得到三角形DEF,若CF=2cm,则BE=2cm.
如图,将三角形ABC沿BC方向平移得到三角形DEF,若CF=2cm,则BE=2cm.