题目内容
10.已知反比例函数y=$\frac{{m}^{2}+m-3}{{x}^{{m}^{2}+2m-2}}$的图象的两个分支分布在第二、四象限,求m的值.分析 就反比例函数的图象在二、四象限得到m2+m-3<0,且m2+2m-2=-1,由此即可解决问题.
解答 解:由题意$\left\{\begin{array}{l}{{m}^{2}+m-3<0}\\{{m}^{2}+2m-2=1}\end{array}\right.$解得m=-3.
所以m=-3.
点评 本题考查反比例函数的性质、熟练掌握反比例函数的性质是解题的关键,记住k>0图象在一、三象限,k<0图象在二、四象限,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.体育测试时,一名九年级的学生推铅球,已知铅球所经过的路线为抛物线y=-$\frac{1}{12}$x2+x+$\frac{7}{3}$(单位:米)的一部分,根据关系式回答,该同学的成绩是( )
| A. | $\frac{7}{3}$米 | B. | $\frac{16}{3}$米 | C. | 14米 | D. | 6米 |
19.对于函数y=-$\frac{6}{x}$,下列说法错误的是( )
| A. | 它的图象分布在第二、四象限 | B. | 它的图象与直线y=x无交点 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x<0时,y的值随x的增大而减小 |
20.互为相反数的两个数在数轴上对应的点之间距离为a,则这两个数中较大的数为( )
| A. | a | B. | -a | C. | $\frac{a}{2}$ | D. | -$\frac{a}{2}$ |
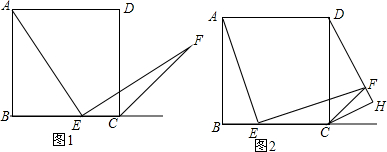
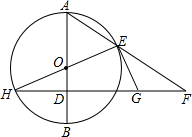 经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F.
经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F.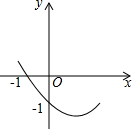 如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.