题目内容
5.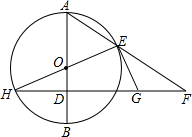 经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F.
经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F.(1)判断△EFG是什么三角形,说明理由;
(2)如果AE=EF,求△EFG三边的比.
分析 (1)由于EG是⊙O的切线,HE是⊙O的直径,得到∠HEG=90°,根据余角的性质得到∠A+∠F=90°,等量代换得到∠GEF=∠F,于是得到结论;
(2)设⊙O与HF交于M,连接DE,EM,根据直角三角形的性质得到DE=EF,DH=DM,于是得到HD=DM=MF,根据三角形的中位线的性质得到EM=2OD=$\frac{1}{2}$AD,设OD=x,则EM=2x,AD=4x,根据勾股定理得到HM=DF=$\sqrt{(6x)^{2}-(2x)^{2}}$=4$\sqrt{2}$x,DE=$\sqrt{D{M}^{2}+E{M}^{2}}$=2$\sqrt{3}$x,推出△EFG∽△DEF,于是得到结论.
解答 解:(1)△EFG是等腰三角形,
理由:∵EG是⊙O的切线,HE是⊙O的直径,
∴∠HEG=90°,
∴∠AEO+∠GEF=90°,
∵HF⊥AB,
∴∠A+∠F=90°,
∵OA=OE,
∴∠A=∠AEO,
∴∠GEF=∠F,
∴△EFG是等腰三角形;
(2)设⊙O与HF交于M,连接DE,EM,
∵HE是⊙O的直径,
∴EM⊥HF,
∵AE=EF,AD⊥HF,
∴DE=EF,DH=DM,
∴HD=DM=MF,
∵EM⊥HF,AD⊥HF,
∴OD∥EM,
∴EM=2OD=$\frac{1}{2}$AD,
设OD=x,则EM=2x,AD=4x,
∴AB=HE=6x,
∴HM=DF=$\sqrt{(6x)^{2}-(2x)^{2}}$=4$\sqrt{2}$x,
∴DE=$\sqrt{D{M}^{2}+E{M}^{2}}$=2$\sqrt{3}$x,
∴EF=DE=2$\sqrt{3}$x,
∵∠EDF=∠F=∠FEG,
∴△EFG∽△DEF,
∴△EFG三边的比为:$\sqrt{3}$:$\sqrt{3}$:2$\sqrt{2}$.
点评 本题考查了切线的性质,勾股定理,相似三角形的判定和性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.

| A. | a2•a5=a10 | B. | a3+a3=a6 | C. | (a3)2=a6 | D. | (2a)3=6a3 |
 如图,在菱形ABCD中,∠A=60°,点E,F分别是边AB,AD上的点,且满足∠BCE=∠DCF,连结EF.
如图,在菱形ABCD中,∠A=60°,点E,F分别是边AB,AD上的点,且满足∠BCE=∠DCF,连结EF.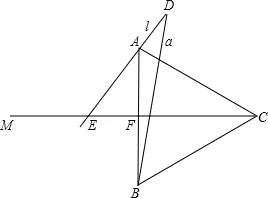 如图所示,已知正△ABC中射线CM⊥AB于F,射线BA绕B顺时针旋转,旋转后的射线记作a,同时线段AB所在直线绕A顺时针旋转,旋转后的直线记作直线l,当直线l旋转的角度是射线a旋转角度的4倍时,直线l于射线CM相交于E,与射线a相交于D,且∠D=30°.
如图所示,已知正△ABC中射线CM⊥AB于F,射线BA绕B顺时针旋转,旋转后的射线记作a,同时线段AB所在直线绕A顺时针旋转,旋转后的直线记作直线l,当直线l旋转的角度是射线a旋转角度的4倍时,直线l于射线CM相交于E,与射线a相交于D,且∠D=30°.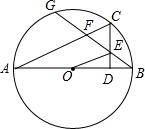 如图,AB是⊙O的直径,C是$\widehat{BG}$的中点,CD⊥AB于D,BG交CD、AC与E、F.求证:
如图,AB是⊙O的直径,C是$\widehat{BG}$的中点,CD⊥AB于D,BG交CD、AC与E、F.求证: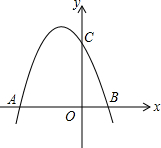 如图抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3),
如图抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3),