题目内容
 如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.
如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.考点:圆周角定理,全等三角形的判定与性质,三角形中位线定理
专题:
分析:作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=
BF=3.
| 1 |
| 2 |
解答:
解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴
=
,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵CA=AF,
∴AH为△CBF的中位线,
∴AH=
BF=3.
∴点A到弦BC的距离为:3.
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,

∴
 |
| DE |
 |
| BF |
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵CA=AF,
∴AH为△CBF的中位线,
∴AH=
| 1 |
| 2 |
∴点A到弦BC的距离为:3.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和三角形中位线性质.

练习册系列答案
相关题目
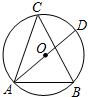 郑州某小区新建一个圆形人工湖,如图所示,弦AB是湖上一座桥,已知桥AB长为200米,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )
郑州某小区新建一个圆形人工湖,如图所示,弦AB是湖上一座桥,已知桥AB长为200米,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )A、100
| ||
B、200
| ||
C、300
| ||
D、400
|
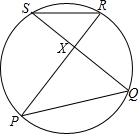 已知P、Q、R、S在圆上,PR与QS相交于X,三角形RSX的面积为1.2,PX=3SX.则三角形PQX的面积为
已知P、Q、R、S在圆上,PR与QS相交于X,三角形RSX的面积为1.2,PX=3SX.则三角形PQX的面积为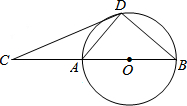 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.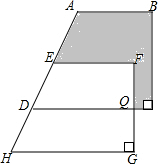 如图,两个直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移距离为AE的长度,其中HG=20cm,QC=5cm,QG=8cm,求阴影部分的面积.
如图,两个直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移距离为AE的长度,其中HG=20cm,QC=5cm,QG=8cm,求阴影部分的面积. 如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.