题目内容
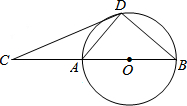 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=
| 2 |
| 3 |
考点:切线的判定
专题:证明题
分析:(1)连接OD,如图,先证明∠CDA=∠ODB,再根据圆周角定理得∠ADO+∠ODB=90°,则∠ADO+∠CDA=90°,即∠CDO=90°,于是根据切线的判定定理即可得到结论;
(2)由于∠CDA=∠ODB,则tan∠CDA=tan∠ABD=
,根据正切的定义得到tan∠ABD=
=
,接着证明△CAD∽△CDB,由相似的性质得
=
=
,然后根据比例的性质可计算出CD的长.
(2)由于∠CDA=∠ODB,则tan∠CDA=tan∠ABD=
| 2 |
| 3 |
| AD |
| BD |
| 2 |
| 3 |
| CD |
| BC |
| AD |
| BD |
| 2 |
| 3 |
解答:
(1)证明:连接OD,如图,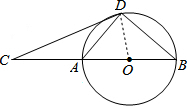
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB是⊙O的直径,
∴∠ADB=90°,即∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的长线;
(2)解:∵∠CDA=∠ODB,
∴tan∠CDA=tan∠ABD=
,
在Rt△ABD中,tan∠ABD=
=
,
∵∠DAC=∠BAD,∠CDA=∠CBD,
∴△CAD∽△CDB,
∴
=
=
,
∴CD=
×6=4.

∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB是⊙O的直径,
∴∠ADB=90°,即∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的长线;
(2)解:∵∠CDA=∠ODB,
∴tan∠CDA=tan∠ABD=
| 2 |
| 3 |
在Rt△ABD中,tan∠ABD=
| AD |
| BD |
| 2 |
| 3 |
∵∠DAC=∠BAD,∠CDA=∠CBD,
∴△CAD∽△CDB,
∴
| CD |
| BC |
| AD |
| BD |
| 2 |
| 3 |
∴CD=
| 2 |
| 3 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
学校以年线为单位开展广播操比赛,全年级有13个班级,每个班级有50名学生,规定班抽25名学生参加比赛,这时样本容量是( )
| A、13 | B、50 |
| C、325 | D、650 |
一个事件发生的概率不可能是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |
 如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.
如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.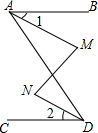 如图,AB∥CD,∠M=∠N,求证:∠1=∠2.
如图,AB∥CD,∠M=∠N,求证:∠1=∠2.