题目内容
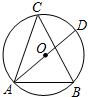 郑州某小区新建一个圆形人工湖,如图所示,弦AB是湖上一座桥,已知桥AB长为200米,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )
郑州某小区新建一个圆形人工湖,如图所示,弦AB是湖上一座桥,已知桥AB长为200米,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )A、100
| ||
B、200
| ||
C、300
| ||
D、400
|
考点:圆周角定理,等腰直角三角形
专题:
分析:连接OB.根据圆周角定理求得∠AOB=90°;然后在等腰Rt△AOB中根据勾股定理求得⊙O的半径AO=OB=100
m,从而求得⊙O的直径AD=200
m
| 2 |
| 2 |
解答:
解:连接OB.
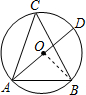
∵∠ACB=45°,∠ACB=
∠AOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠AOB=90°;
在Rt△AOB中,OA=OB(⊙O的半径),AB=200m,
∴由勾股定理得,AO=OB=100
m,
∴AD=2OA=200
m;
故选B.

∵∠ACB=45°,∠ACB=
| 1 |
| 2 |
∴∠AOB=90°;
在Rt△AOB中,OA=OB(⊙O的半径),AB=200m,
∴由勾股定理得,AO=OB=100
| 2 |
∴AD=2OA=200
| 2 |
故选B.
点评:本题主要考查了等腰直角三角形、圆周角定理.利用圆周角定理求直径的长时,常常将直径置于直角三角形中,利用勾股定理解答.

练习册系列答案
相关题目
 一副三角板按如图方式摆放,如果∠2=18°,则∠1=( )
一副三角板按如图方式摆放,如果∠2=18°,则∠1=( )| A、18° | B、54° |
| C、72° | D、70° |
 如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )
如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )| A、70° | B、60° |
| C、55° | D、45° |
 如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.
如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离. 如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?
如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?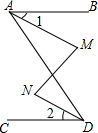 如图,AB∥CD,∠M=∠N,求证:∠1=∠2.
如图,AB∥CD,∠M=∠N,求证:∠1=∠2.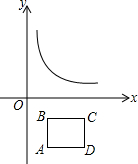 如图,矩形ABCD的边AB=2,BC=4,且BC∥x轴,已知点A的坐标是(2,4).
如图,矩形ABCD的边AB=2,BC=4,且BC∥x轴,已知点A的坐标是(2,4).