题目内容
2.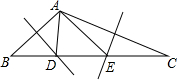 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.(1)若BC=10,则△ADE周长是10;
(2)若∠BAC=128°,则∠DAE的度数是76°.
分析 (1)由在△ABC中,边AB、AC的垂直平分线分别交BC于E、F,易得AE=BE,AF=CF,即可得BC=△AEF周长;
(2)由∠BAC=128°,可求得∠B+∠C的值,即可得∠BAE+∠CAF的值,继而求得答案.
解答 解:(1)∵在△ABC中,边AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF,
∵△ADE周长是10,
∴BC=BE+EF+CF=AE+EF+AF=10;
故答案为:10;
(2)∵AE=BE,AF=CF,
∴∠B=∠BAE,∠C=∠CAF,
∵∠BAC=128°,
∴∠B+∠C=180°-∠BAC=52°,
∴∠BAE+∠CAF=∠B+∠C=52°,
∴∠FAE=∠BAC-(∠BAE+∠CAF)=76°,
故答案为:76°.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
13. 已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
 已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )| A. | 24cm和12cm | B. | 16cm和22cm | C. | 20cm和16cm | D. | 22cm和16cm |
7.已知一个多边形的最小的外角是60°,其余外角依次增加20°,则这个多边形的边数为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
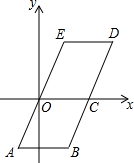 如图,四边形ABCO和OCDE是两个形状相同,大小相等的平行四边形,已知点A(-1,-2),D(4,2),求点B、C、E的坐标及平行四边形ABDE的面积.
如图,四边形ABCO和OCDE是两个形状相同,大小相等的平行四边形,已知点A(-1,-2),D(4,2),求点B、C、E的坐标及平行四边形ABDE的面积.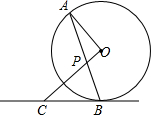 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C. 已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C.
已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C.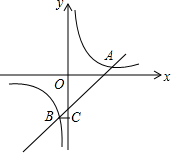 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.