题目内容
1.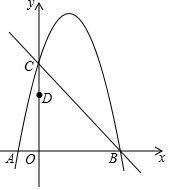 如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).
如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).(1)求抛物线的解析式;
(2)M,N分别是BC,x轴上的动点,求△DMN周长最小时点M,N的坐标,并写出周长的最小值;
(3)连接BD,设M是平面上一点,将△BOD绕点M顺时针旋转90°后得到△B1O1D1,点B,O,D的对应点分别是B1,O1,D1,若△B1O1D1的两个顶点恰好落在抛物线上,请直接写出点O1的坐标.
分析 (1)求出B、C两点坐标,利用待定系数法即可解决问题;
(2)如图1中,作点D关于BC的对称点D′,点D关于x轴的对称点D″,连接D′D″交BC于M,交x轴于N,连接DM,DN.此时△DMN的周长最小.求出D′、D″的坐标,直线D′D″的解析式即可解决问题;
(3)分两种情形①如图2中,当O′和D′在抛物线上时,易知点O′与点C重合,CD′=OD=3,此时O′(0,5).②如图3中,点B′、D′在抛物线上时,设点B′(x,-x2+4x+5)的横坐标为x+1,则点D′的坐标为(x+3,-x2+4x+10).把D′的坐标代入抛物线的解析式,求出x即可解决问题;
解答 解:(1)由题意C(0,5),B(5,0),
把C(0,5),B(5,0)的坐标代入y=-x2+bx+c得到$\left\{\begin{array}{l}{c=5}\\{-25+5b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=4}\\{c=5}\end{array}\right.$,
∴抛物线的解析式为y=-x2+4x+5.
(2)如图1中,作点D关于BC的对称点D′,点D关于x轴的对称点D″,连接D′D″交BC于M,交x轴于N,连接DM,DN.此时△DMN的周长最小.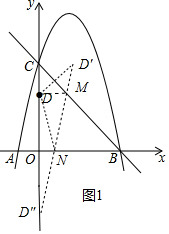
易知D′(2,5),D″(0,-3),
设直线D′D″的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=-3}\\{2k+b=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=4}\\{b=-3}\end{array}\right.$,
∴y=4x-3,
∴N($\frac{3}{4}$,0),
由$\left\{\begin{array}{l}{y=-x+5}\\{y=4x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{8}{5}}\\{y=\frac{17}{5}}\end{array}\right.$,
∴M($\frac{8}{5}$,$\frac{17}{5}$),
∴△DMN周长最小时点M($\frac{8}{5}$,$\frac{17}{5}$),N($\frac{3}{4}$,0),
△DMN的周长的最小值=D′D″=$\sqrt{{2}^{2}+{8}^{2}}$=2$\sqrt{17}$.
(3)①如图2中,当O′和D′在抛物线上时,易知点O′与点C重合,CD′=OD=3,此时O′(0,5).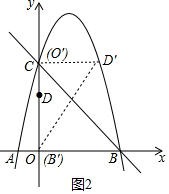
②如图3中,点B′、D′在抛物线上时,设点B′(x,-x2+4x+5)的横坐标为x+1,则点D′的坐标为(x+3,-x2+4x+10).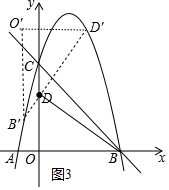
把D′坐标代入y=-x2+4x+5中,得到-x2+4x+10=-(x+3)2+4(x+3)+5,
解得x=-$\frac{1}{3}$,
∴B′(-$\frac{1}{3}$,$\frac{32}{9}$),
∴O′(-$\frac{1}{3}$,$\frac{77}{9}$),
综上所述,满足条件的点O′的坐标为(0,5)或(-$\frac{1}{3}$,$\frac{77}{9}$).
点评 本题考查二次函数综合题、一次函数的应用、待定系数法、轴对称、旋转变换等知识,解题的关键是学会利用轴对称解决最值问题,学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.

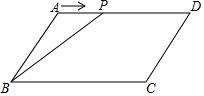 如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )
如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )| A. | y=-4x+2 | B. | y=-4x-2 | C. | y=2$\sqrt{3}$x | D. | y=$\sqrt{3}$x |
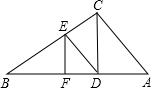 如图,添加一个条件∠BDE=∠A或∠BED=∠BCA或∠EDC=∠DCA或∠CED+∠ECA=180°,使AC∥DE.
如图,添加一个条件∠BDE=∠A或∠BED=∠BCA或∠EDC=∠DCA或∠CED+∠ECA=180°,使AC∥DE.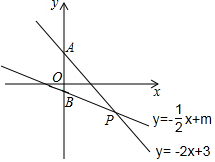 如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于(n,-2).
如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于(n,-2).