题目内容
10.数轴上有两个点A和B,点A表示的数是$\sqrt{3}$,点B与点A相距2个单位长度,则点B所表示的实数是$\sqrt{3}+2$,$\sqrt{3}-2$.分析 根据数轴上到一点距离相等的点有两个,可得答案.
解答 解:∵A点右边的点表示的数是$\sqrt{3}$+2,
A点左边的点表示的数是$\sqrt{3}$-2,
则点B所表示的实数是:$\sqrt{3}+2$,$\sqrt{3}-2$;
故答案为:$\sqrt{3}+2$,$\sqrt{3}-2$.
点评 本题考查了实数与数轴,数轴上到一点距离相等的点有两个,以防遗漏.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20. 如图,将周长为7cm的△ABC沿BC方向向右平移1cm得到△DEF,则四边形ABFD的周长为( )
如图,将周长为7cm的△ABC沿BC方向向右平移1cm得到△DEF,则四边形ABFD的周长为( )
 如图,将周长为7cm的△ABC沿BC方向向右平移1cm得到△DEF,则四边形ABFD的周长为( )
如图,将周长为7cm的△ABC沿BC方向向右平移1cm得到△DEF,则四边形ABFD的周长为( )| A. | 7cm | B. | 8cm | C. | 9cm | D. | 10cm |
18.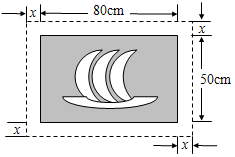 如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
 如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )| A. | x2+130x-1400=0 | B. | x2+65x-350=0 | C. | x2-130x-1400=0 | D. | x2-65x-350=0 |
5. 如图,直线a,b被直线c所截,与∠1是同位角的角是( )
如图,直线a,b被直线c所截,与∠1是同位角的角是( )
 如图,直线a,b被直线c所截,与∠1是同位角的角是( )
如图,直线a,b被直线c所截,与∠1是同位角的角是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
15.若不等式5x-k≤0的正整数解是1、2、3,则k的取值范围是( )
| A. | m≥15 | B. | 15<k≤20 | C. | 15≤k≤20 | D. | 15≤k<20 |
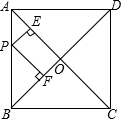 如图,在正方形ABCD中,对角线BD长为18cm,P是AB上任意一点,则点P到AC、BD的距离之和等于9cm.
如图,在正方形ABCD中,对角线BD长为18cm,P是AB上任意一点,则点P到AC、BD的距离之和等于9cm.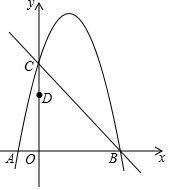 如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).
如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).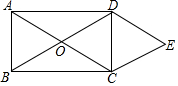 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2.求四边形OCED的面积.
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2.求四边形OCED的面积.