题目内容
10.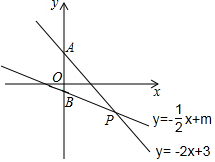 如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于(n,-2).
如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于(n,-2).(1)求出m、n的值;
(2)求出△ABP的面积.
分析 (1)根据直线AP的解析式结合点P的纵坐标即可得出n的值,由此可得出点P的坐标,再根据点P的坐标利用待定系数法即可求出m的值;
(2)根据一次函数图象上点的坐标特征求出点A、B的坐标,再根据三角形的面积公式即可求出△ABP的面积.
解答 解:(1)∵点P(n,-2)在一次函数y=-2x+3的图象上,
∴-2=-2n+3,
解得:n=$\frac{5}{2}$,
∴点P的坐标为($\frac{5}{2}$,-2).
∵点P($\frac{5}{2}$,-2)在一次函数y=-$\frac{1}{2}$x+m的图象上,
∴-2=-$\frac{1}{2}$×$\frac{5}{2}$+m,
解得:m=-$\frac{3}{4}$.
(2)当x=0时,y=-2x+3=3,
∴点A的坐标为(0,3);
当x=0时,y=-$\frac{1}{2}$x-$\frac{3}{4}$=-$\frac{3}{4}$,
∴点B的坐标为(0,-$\frac{3}{4}$),
∴AB=3-(-$\frac{3}{4}$)=$\frac{15}{4}$,
∴S△ABP=$\frac{1}{2}$AB•xP=$\frac{1}{2}$×$\frac{15}{4}$×$\frac{5}{2}$=$\frac{75}{16}$.
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及三角形的面积,解题的关键是:(1)利用一次函数图象上点的坐标特征求出点P的坐标;(2)利用一次函数图象上点的坐标特征求出点A、B的坐标.

练习册系列答案
相关题目
18.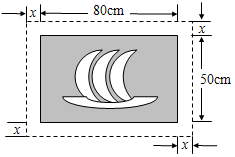 如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
 如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )| A. | x2+130x-1400=0 | B. | x2+65x-350=0 | C. | x2-130x-1400=0 | D. | x2-65x-350=0 |
20.下列事件属于不可能事件的是( )
| A. | 两个数的和小于0 | B. | 一个数的相反数等于它本身 | ||
| C. | 一个数的绝对值小于0 | D. | 两个负数的积大于0 |
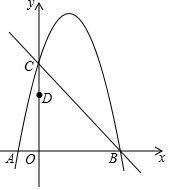 如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).
如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).
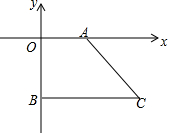 如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.
如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.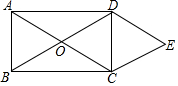 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2.求四边形OCED的面积.
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2.求四边形OCED的面积.