题目内容
5.已知:∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线,(1)如图1,若OM平分∠AOB,ON平分∠DOB,当OB绕点O在∠AOD内旋转时,求∠MON的大小.
(2)如图2.若∠BOC=20°,OM平分∠AOC,ON平分∠DOB,当∠COB绕点O在∠AOD内旋转时,求∠MON的大小.
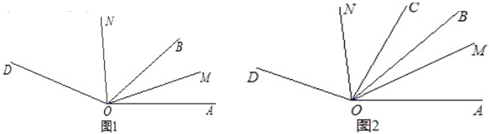
分析 (1)若OM平分∠AOB、ON平分∠BOD,则∠MOB=$\frac{1}{2}$∠AOB、∠BON=$\frac{1}{2}$∠BOD.然后根据∠MON=∠MOB+∠BON转化求出角的度数;
(2)由OM平分∠AOC、ON平分∠DOB知∠MOC=$\frac{1}{2}$∠AOC、∠BON=$\frac{1}{2}$∠BOD,然后根据∠MON=∠MOC+∠BON-∠BOC转化求出角的度数;
解答 解:(1)∵∠AOD=160°,OM平分∠AOB,ON平分∠BOD
∴∠MOB=$\frac{1}{2}$∠AOB,∠BON=$\frac{1}{2}$∠BOD
即∠MON=∠MOB+∠BON
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOD
=$\frac{1}{2}$(∠AOB+∠BOD)
=$\frac{1}{2}$∠AOD
=80°;
(2)∵OM平分∠AOC,ON平分∠BOD
∴∠MOC=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD
即∠MON=∠MOC+∠BON-∠BOC
=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD-∠BOC
=$\frac{1}{2}$(∠AOC+∠BOD)-∠BOC
=$\frac{1}{2}$×180°-20°
=70°.
点评 本题主要考查角平分线及角的和差计算,根据角平分线定义得出所求角与已知角的关系转化,然后根据已知条件求解是关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
7.如图,点A在直线l上,BA⊥CA,∠1=40°,则∠2的度数为( )


| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
17. 如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )
如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )
 如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )
如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{2}{5}$ | C. | $\sqrt{2}-1$ | D. | 2$-\sqrt{2}$ |
 如图,直线a∥b,∠1=110°,∠2=65°,则∠3的度数为45°.
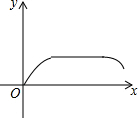
如图,直线a∥b,∠1=110°,∠2=65°,则∠3的度数为45°. 如图,矩形MDBN从B点匀速向右运动,当B点与C点重合时停止,设移动的时间为x,两图形重合的面积为y,则y关于x的函数图象是( )
如图,矩形MDBN从B点匀速向右运动,当B点与C点重合时停止,设移动的时间为x,两图形重合的面积为y,则y关于x的函数图象是( )


 已知二次函数y=2x2-x-3.
已知二次函数y=2x2-x-3. 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=55°,∠B=30°,则∠BDC的度数为80°.
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=55°,∠B=30°,则∠BDC的度数为80°.