题目内容
10．若$\sqrt{3+m}+{（n-1）^2}$=0，则m+n的值为-2．分析 根据任何数的算术平方根以及偶次方都是非负数，几个非负数的和是0，则每个数等于0，据此列方程求的m和n的值，进而求的代数式的值．
解答 解：根据题意得：$\left\{\begin{array}{l}{3+m=0}\\{n-1=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=-3}\\{n=1}\end{array}\right.$，
则m+n=-3+1=-2．
故答案是：-2．
点评 本题考查了非负数的性质，初中范围内的非负数有：任何数的算术平方根、偶次方以及绝对值三个，几个非负数的和是0，则每个数等于0．
练习册系列答案
相关题目
如图，A，B两地之间有一座山，汽车原来从A地道B地须经C地沿折线A-C-B行驶，全长68km，现开通隧道后，汽车直接沿直线AB行驶．已知∠A=30°，∠B=45°，则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果精确到0.1km）（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）
1．下列由线段a，b，c组成的三角形不是直角三角形的是（ ）
| A． | a=3，b=4，c=5 | B． | a=2$\sqrt{13}$，b=3，c=$\sqrt{43}$ | C． | a=12，b=10，c=20 | D． | a=5，b=13，c=12 |
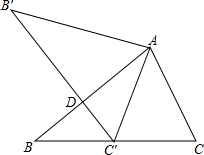如图，将△ABC绕点A顺时针旋转60°后，得△AB′C，且C′为BC的中点，则$\frac{B′D}{AB′}$=$\frac{\sqrt{3}}{2}$．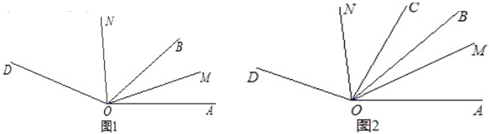
在某次学校安全知识抢答赛中，九年级参赛的10名学生的成绩统计图如图所示．这10名学生的参赛成绩的中位数是90分．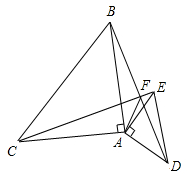
等腰直角△ABC与等腰直角△ADE中，AB=AC，AD=AE，∠BAC=90°，∠DAE=90°，如图，将△ADE绕点A旋转一定度数，连BD、EC，BD与EC交于点F，连AF．求证：