题目内容
解方程:
(1)
=
(2)
-
=0
(3)
=
-
.
(1)
| 2 |
| x-1 |
| 3 |
| x |
(2)
| 5 |
| y2+y |
| 1 |
| y2-y |
(3)
| 5x-4 |
| 2x-4 |
| 2x+5 |
| 3x-6 |
| 1 |
| 2 |
考点:解分式方程
专题:计算题
分析:分式方程去分母转化为整式方程,求出整式方程的解得到未知数的值,代入检验即可得到分式方程的解.
解答:解:(1)去分母得:2x=3x-3,
解得:x=3,
经检验x=3是分式方程的解;
(2)去分母得:5y2-5y=y2+y,即2y(2y-3)=0,
解得:y=0或y=1.5,
经检验y=0是增根,分式方程的解为y=1.5;
(3)去分母得:15x-12=4x+10-3x+6,
移项合并得:14x=28,
解得:x=2,
经检验x=2是增根,分式方程无解.
解得:x=3,
经检验x=3是分式方程的解;
(2)去分母得:5y2-5y=y2+y,即2y(2y-3)=0,
解得:y=0或y=1.5,
经检验y=0是增根,分式方程的解为y=1.5;
(3)去分母得:15x-12=4x+10-3x+6,
移项合并得:14x=28,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
如果
=
成立,则x的范围( )
| ||
|
|
| A、x≥0 | B、x≥1 |
| C、0<x≤1 | D、x>0 |
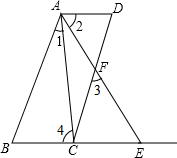 如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.
如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.证明:∵AD∥BE,
∴∠4=
∵∠1=∠2.
∴∠1+∠CAE=∠2+
即∠BAE=
∵AB∥CD,
∴∠3=
∴∠3=
 2014年巴西世界杯是第20届世界杯足球赛,比赛于2014年6月12日至7月13日在南美洲国家巴西境内举行.给全世界足球爱好者带来了一场足球盛宴.足球一般是有黑白两种颜色的皮块缝制而成,如图所示,黑色皮块是正五边形,白色皮块是正六边形,若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为( )
2014年巴西世界杯是第20届世界杯足球赛,比赛于2014年6月12日至7月13日在南美洲国家巴西境内举行.给全世界足球爱好者带来了一场足球盛宴.足球一般是有黑白两种颜色的皮块缝制而成,如图所示,黑色皮块是正五边形,白色皮块是正六边形,若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为( )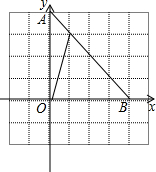 如图,等腰直角△AOB中,∠AOB=90°,点D在AB上,将△AOD绕顶点O沿顺时针方向旋转90°后得到△BOE.
如图,等腰直角△AOB中,∠AOB=90°,点D在AB上,将△AOD绕顶点O沿顺时针方向旋转90°后得到△BOE. 如图,有一条等宽的纸带,按如图所示进行折叠,求纸带重叠部分中的∠α的度数.
如图,有一条等宽的纸带,按如图所示进行折叠,求纸带重叠部分中的∠α的度数.
 如图,在△ABC中,D是AB边上一点,且AD:DB=5:3,过点D作DE∥BC,交边AC于点E,那么ED用BC可表示为
如图,在△ABC中,D是AB边上一点,且AD:DB=5:3,过点D作DE∥BC,交边AC于点E,那么ED用BC可表示为