题目内容
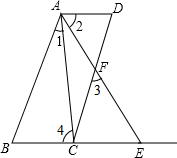 如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.
如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.证明:∵AD∥BE,
∴∠4=
∵∠1=∠2.
∴∠1+∠CAE=∠2+
即∠BAE=
∵AB∥CD,
∴∠3=
∴∠3=
考点:平行线的性质
专题:推理填空题
分析:由平行可求得∠4=∠2+∠CAE=∠1+∠CAE=∠BAE=∠3,可证得结论,据此填空即可.
解答:证明:∵AD∥BE,
∴∠4=∠CAD( 两直线平行,内错角相等),
∵∠1=∠2.
∴∠1+∠CAE=∠2+∠CAE.
即∠BAE=∠CAD.
∵AB∥CD,
∴∠3=∠BAE( 两直线平行,同位角相等),
∴∠3=∠4.
故答案为:∠CAD;两直线平行,内错角相等;∠CAE;∠CAD;∠BAE;两直线平行,同位角相等;∠4.
∴∠4=∠CAD( 两直线平行,内错角相等),
∵∠1=∠2.
∴∠1+∠CAE=∠2+∠CAE.
即∠BAE=∠CAD.
∵AB∥CD,
∴∠3=∠BAE( 两直线平行,同位角相等),
∴∠3=∠4.
故答案为:∠CAD;两直线平行,内错角相等;∠CAE;∠CAD;∠BAE;两直线平行,同位角相等;∠4.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图表示字母a的取值范围,这个范围是( )
如图表示字母a的取值范围,这个范围是( )| A、a>2 | B、a≥2 |
| C、a<2 | D、a≤2 |
化简x(2x-1)-x2(2-x)的结果是( )
| A、-x3-x |
| B、x3-x |
| C、-x2-1 |
| D、x3-1 |
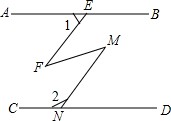 如图,AB∥CD,∠1+∠2=180°,试给出∠EFM与∠NMF的大小关系,并证明你的结论.
如图,AB∥CD,∠1+∠2=180°,试给出∠EFM与∠NMF的大小关系,并证明你的结论.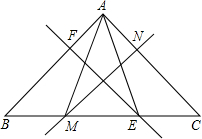 如图所示,在△ABC中,∠BAC=76°,EF,MN分别是AB,AC的垂直平分线,点E,M在BC上,则∠EAM=
如图所示,在△ABC中,∠BAC=76°,EF,MN分别是AB,AC的垂直平分线,点E,M在BC上,则∠EAM=