题目内容
若关于x的方程x2-34x+34k-1=0至少有1个正整数根,求正整数k的值.
考点:根的判别式
专题:
分析:根据已知条件得出△≥0,求出k的取值范围,再根据k为正整数,求出k的值,再找出使方程至少有1个正整数根的值即可.
解答:解:∵方程x2-34x+34k-1=0至少有1个正整数根,
∴△=342-4(34k-1)=1160-136k≥0,
解得:k可能取值为1,2,3,4,5,6,7,8,
∵只有当k=1时,x1=1,x2=33,
∴正整数k的值是1.
∴△=342-4(34k-1)=1160-136k≥0,
解得:k可能取值为1,2,3,4,5,6,7,8,
∵只有当k=1时,x1=1,x2=33,
∴正整数k的值是1.
点评:此题考查了根的判别式,掌握好一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
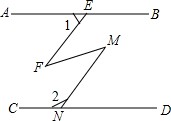 如图,AB∥CD,∠1+∠2=180°,试给出∠EFM与∠NMF的大小关系,并证明你的结论.
如图,AB∥CD,∠1+∠2=180°,试给出∠EFM与∠NMF的大小关系,并证明你的结论.