题目内容
 如图,有一条等宽的纸带,按如图所示进行折叠,求纸带重叠部分中的∠α的度数.
如图,有一条等宽的纸带,按如图所示进行折叠,求纸带重叠部分中的∠α的度数.考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:如图,由条件可知AB∥CD,可得∠EFC=∠AEH,∠GFD=∠AGF,由折叠可得到∠EFG=∠GFD,可求得∠α.
解答: 解:∵AB∥CD,
解:∵AB∥CD,
∴∠EFC=∠AEH=70°,∠α=∠GFD,
又∵由折叠的性质可得∠EFG=∠GFD,且∠EFC+∠EFD=180°,
∴∠GFD=
(180°-∠EFC)=55°,
∴∠α=55°
 解:∵AB∥CD,
解:∵AB∥CD,∴∠EFC=∠AEH=70°,∠α=∠GFD,
又∵由折叠的性质可得∠EFG=∠GFD,且∠EFC+∠EFD=180°,
∴∠GFD=
| 1 |
| 2 |
∴∠α=55°
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,已知AB∥CD,BE平分∠ABD,DE平分∠CDB,求证:BE⊥DE.
如图,已知AB∥CD,BE平分∠ABD,DE平分∠CDB,求证:BE⊥DE.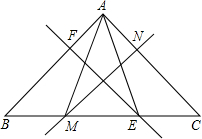 如图所示,在△ABC中,∠BAC=76°,EF,MN分别是AB,AC的垂直平分线,点E,M在BC上,则∠EAM=
如图所示,在△ABC中,∠BAC=76°,EF,MN分别是AB,AC的垂直平分线,点E,M在BC上,则∠EAM=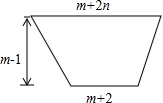 如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值.
如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值.