题目内容
17.是否存在这样的正整数a,使方程组$\left\{\begin{array}{l}{x-y=2a}\\{x+3y=1-5a}\end{array}\right.$的解x与y都是正数?如果存在,请求出这个方程组的解;如果不存在,请说明理由.分析 把a看做已知数表示出方程组的解,由x与y都是正数,列出不等式组,求出不等式组的解集确定出a的范围,进而求出正整数a的值,即可求出方程组的解.
解答 解:$\left\{\begin{array}{l}{x-y=2a①}\\{x+3y=1-5a②}\end{array}\right.$,
②-①得:4y=1-7a,即y=$\frac{1-7a}{4}$③,
把③代入①得:x=$\frac{1+a}{4}$,
由题意得:$\left\{\begin{array}{l}{\frac{1-7a}{4}>0}\\{\frac{1+a}{4}>0}\end{array}\right.$,
解得:-1<a<$\frac{1}{7}$,
由a为正整数,得到a=0,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{1}{4}}\\{y=\frac{1}{4}}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
7.在Rt△ABC中,AB=3,AC=4,则BC的长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 无法确定 |
2.某工厂的大门是抛物线型水泥建筑物,大门地面宽为8m,两侧距地面3m处各有一个壁灯,两壁灯之间的水平距离为6m,则大门的高约为( )
| A. | 6.9m | B. | 7.0m | C. | 7.1m | D. | 6.8m |
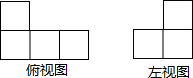 如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.
如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.