Question

11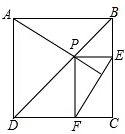．在正方形ABCD中，P是BD上一点，过P引PE⊥BC交BC于E，过P引PF⊥CD于F，求证：AP⊥EF．

Answer 1

分析 延长FP交AB交于G，延长AP交EF于点H，易证△PAG≌△EFP，可求得∠FPH+∠PFH=90°，可证得结论．

解答 证明：如图，

延长FP交AB于点G，AP交EF于点H，
∵四边形ABCD为正方形，
∴∠C=∠ABC=90°，
又∵PE⊥BC，PF⊥CD，
∴四边形PECF为矩形，
同理四边形BCFG也为矩形，
∴PE=FC=GB，
又∵BD平分∠ABC，
∴∠GBD=45°，
∴PG=BG=PE，
又∵AB=BC=CD，
∴AG=EC=PF，
在△PAG和△EFP中，$\left\{\begin{array}{l}{AG=PF}\\{∠AGP=∠FPE}\\{PG=PE}\end{array}\right.$，
∴△PAG≌△EFP（SAS），
∴∠APG=∠FEP=∠FPH，
∵∠FEP+∠PFH=90°，
∴∠FPH+∠PFH=90°，
∴AP⊥EF

点评 本题主要考查正方形的性质及全等三角形的判定和性质，构造三角形全等找到角之间的关系是解题的关键．