题目内容
20．
已知如图，在⊙O中，AB是⊙O的直径，AC、BC分别交⊙O于E、D，D是BE的中点，∠A=40°，求∠C的大小．
分析 由圆周角定理求出∠ADB=90°，由线段垂直平分线的性质得出AB=AC，再由三角形内角和定理即可得出结果．
解答 解：连接AD，
如图所示：
∵AB为⊙O的直径，
∴∠ADB=90°，
即AD⊥BC，
又∵D是BE的中点，
∴AB=AC，
∴∠C=∠B=$\frac{1}{2}$（180°-∠A）=70°．
点评 此题考查了圆周角定理，等腰三角形的性质，三角形内角和定理；熟练掌握圆周角定理是解本题的关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
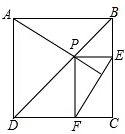在正方形ABCD中，P是BD上一点，过P引PE⊥BC交BC于E，过P引PF⊥CD于F，求证：AP⊥EF．
如图，已知直线l：y=2x，分别过x轴上的点A1（1，0）、A2（2，0）、…、An（n，0），作垂直于x轴的直线交l于点B1、B2、…、Bn，将△OA1B1，四边形A1A2B2B1、…、四边形An-1AnBnBn-1的面积依次记为S1、S2、…、Sn，则Sn=（ ）