题目内容
2.点P是∠AOB内的一点,PA⊥OA,PB⊥OB,垂足分别为点A,B,且PA=PB,点C是射线OA上不与点A重合的一点,点D是射线OB上不与点B重合的一点,且AC=BD,下列结论不一定成立的是( )| A. | OA=OB | B. | PO平分∠APB | C. | OC=OD | D. | △PAC≌△PBD |
分析 利用角平分线的性质,全等三角形的判定即可.
解答 解:如图1,
∵PA⊥OA,PB⊥OB,垂足分别为点A,B,且PA=PB,
∴∠AOP=∠BOP,
在Rt△AOP和Rt△BOP中$\left\{\begin{array}{l}{PA=PB}\\{OP=OP}\end{array}\right.$
∴Rt△OAP≌Rt△OBP,
∴OA=OB,∠APO=∠BPO,
∴PO平分∠APB,
∴A、B正确,
如图2,
在△APC和△BPD中$\left\{\begin{array}{l}{AC=BD}\\{∠CAP=∠DBP=90°}\\{PA=PB}\end{array}\right.$,
∴△APC≌△BPD,
∴同理:△APC≌△BPD',△APC'≌△BPD',△APC'≌△BPD,
∴D正确,
①点C在线段OA上,点D在线段OB上,OC=OA-AC,OD=OB-BD,∴OC=OD,
同理:②点C'在射线OA上,点D'在射线OB上,OC'=OD',
③点C在线段OA上,点D'在射线OB上,OC=OA-AC,OD'=OB+BD',∴OC≠OD',
同理:④点C'在射线OA上,点D在线段OB上,OC'≠OD,∴C错误.
故选C.
点评 此题是全等三角形的判定和性质,主要考查了角平分线的性质,解本题的关键是作出图形,也是本题的难点.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 平面直角坐标系中,点P(3a+1,6a-5)是第一、三象限的角平分线上的点,点C(0,m)、D(n,0),m≠0,∠CPD=90°
平面直角坐标系中,点P(3a+1,6a-5)是第一、三象限的角平分线上的点,点C(0,m)、D(n,0),m≠0,∠CPD=90° 如图,△ABC中,AB=AC,点D为BC的中点,∠BAD=50°,则∠C=40°.
如图,△ABC中,AB=AC,点D为BC的中点,∠BAD=50°,则∠C=40°. 如图,Rt△ABC中,∠C=90°,b=4$\sqrt{5}$,∠A的平分线AD=$\frac{8\sqrt{15}}{3}$,解此三角形.
如图,Rt△ABC中,∠C=90°,b=4$\sqrt{5}$,∠A的平分线AD=$\frac{8\sqrt{15}}{3}$,解此三角形.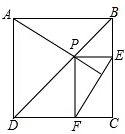 在正方形ABCD中,P是BD上一点,过P引PE⊥BC交BC于E,过P引PF⊥CD于F,求证:AP⊥EF.
在正方形ABCD中,P是BD上一点,过P引PE⊥BC交BC于E,过P引PF⊥CD于F,求证:AP⊥EF.