题目内容
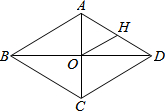如图所示，菱形ABCD中，对角线AC、BD相交于点O，H为AD边的中点，菱形ABCD的周长为36，则OH的长等于（ ）| A、4.5 | B、5 | C、6 | D、9 |
考点：菱形的性质,直角三角形斜边上的中线,三角形中位线定理
专题：
分析：可先求得AB的长，再根据三角形中位线定理可求得OH的长．
解答：解：∵四边形ABCD为菱形，且周长为36，
∴AB=BC=CD=AD=9，
又∵O为BD中点，H为AD的中点，
∴OH为△ABD的中位线，
∴OH=
AB=4.5，
故选A．
∴AB=BC=CD=AD=9，
又∵O为BD中点，H为AD的中点，
∴OH为△ABD的中位线，
∴OH=
| 1 |
| 2 |
故选A．
点评：本题主要考查菱形的性质，掌握菱形的四边相等、对角线互相垂直平分是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，矩形ABCD中，AB=1，AD=a，以点A为圆心，a为半径画弧，交BC于点E，交AB延长线于点F，当两个阴影部分面积相等时，a的值是
如图所示的各边相等的正五角星中，∠A=α、∠CGH=β、∠HIJ=γ，则α：β：γ=
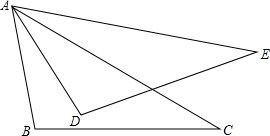如图，使△ABC≌△ADE的条件是（ ）| A、∠BAC=∠DAE，∠ABC=∠ADE，∠ACB=∠AED |
| B、∠BAC=∠DAE，AB=AD，BC=DE |
| C、∠BAD=∠CAE，AB=AD，AC=AE |
| D、∠ACB=∠AED，AB=AD，AC=AE |
如图，在梯形ABCD中，AB∥CD，AD=DC=BD=a，BC=b，求AC的长．
在平行四边形ABCD中，AC为对角线，BE垂直于AC于E，DF垂直于AC于F．
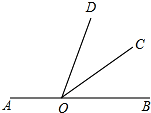如图，点O在直线AB上，射线OC平分∠DOB，若∠COB=36°，则∠AOD等于（ ）| A、72° | B、100° |
| C、108° | D、144° |
下列图形中，是轴对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |