题目内容
 在平行四边形ABCD中,AC为对角线,BE垂直于AC于E,DF垂直于AC于F.
在平行四边形ABCD中,AC为对角线,BE垂直于AC于E,DF垂直于AC于F.(1)求证:四边形BFDE为平行四边形.
(2)连结BD,若BD与AC的交点为O,求证:OE=OF.
考点:平行四边形的判定与性质
专题:证明题
分析:(1)首先利用平行四边形的性质得出AB=CD,∠BAC=∠DCF,进而得出△ABE≌△CDF(AAS),即可得出BE=DF,然后根据BE∥DF即可证得;
(2)根据平行四边形的对角线互相平分即可证得.
(2)根据平行四边形的对角线互相平分即可证得.
解答: 证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCF,
∵BE⊥AC,DF⊥AC,
∴∠BEA=∠DFC,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF.
又∵BE∥DF,
∴四边形BFDE为平行四边形;
(2)连接BD.
∵四边形BFDE为平行四边形,
∴OE=OF.
 证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
∴∠BAC=∠DCF,
∵BE⊥AC,DF⊥AC,
∴∠BEA=∠DFC,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(AAS),
∴BE=DF.
又∵BE∥DF,
∴四边形BFDE为平行四边形;
(2)连接BD.
∵四边形BFDE为平行四边形,
∴OE=OF.
点评:本题考查了平行四边形的判定与性质,正确依据全等三角形的性质证明BE=DF是关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 下列四个图案中,可以通过如图平移得到的是( )
下列四个图案中,可以通过如图平移得到的是( )A、 |
B、 |
C、 |
D、 |
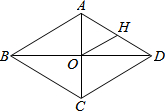 如图所示,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形ABCD的周长为36,则OH的长等于( )
如图所示,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形ABCD的周长为36,则OH的长等于( )| A、4.5 | B、5 | C、6 | D、9 |
-
与
在数轴上对应点的位置如图所示,则数轴上被圈住的表示整数的点的个数为( 
| 2 |
| 10 |

| A、2个 | B、3个 | C、4个 | D、5个 |
在锐角三角形ABC中,BC>AB>AC,小靖依下列方法作图:
(1)作∠A的平分线交BC于D点.
(2)作AD的中垂线交AC于E点.
(3)连接DE.
根据他画的图形,下列关系正确的是( )
(1)作∠A的平分线交BC于D点.
(2)作AD的中垂线交AC于E点.
(3)连接DE.
根据他画的图形,下列关系正确的是( )
| A、DE∥AB |
| B、DE⊥AC |
| C、CD=DE |
| D、CD=BD |
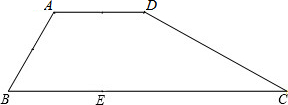
 如图是某滑板俱乐部训练时的斜坡截面的示意图,该截面垂直于地面,出于安全因素考虑,俱乐部决定将训练的斜坡AB改造成FD,这时斜坡的倾角由45°降为30°,坡顶加宽的长度AF为1m,已知原斜坡面AB唱为6
如图是某滑板俱乐部训练时的斜坡截面的示意图,该截面垂直于地面,出于安全因素考虑,俱乐部决定将训练的斜坡AB改造成FD,这时斜坡的倾角由45°降为30°,坡顶加宽的长度AF为1m,已知原斜坡面AB唱为6
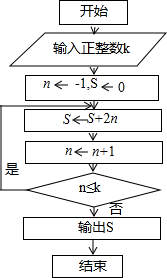 在计算机科学中常用框图表示程序运行的顺序,称程序流程图.(如图所示,箭头表示执行的顺序或数据的流向,如n←n+1表示将n的值增加1后仍赋给n)执行如图的流程图,如果输入的K=10,那么输出的S=
在计算机科学中常用框图表示程序运行的顺序,称程序流程图.(如图所示,箭头表示执行的顺序或数据的流向,如n←n+1表示将n的值增加1后仍赋给n)执行如图的流程图,如果输入的K=10,那么输出的S=