题目内容
如图所示的各边相等的正五角星中，∠A=α、∠CGH=β、∠HIJ=γ，则α：β：γ=考点：多边形内角与外角,等腰三角形的性质
专题：
分析：根据五边形FGHIJ是正五边形，即可求得∠γ的度数，然后利用三角形内角和定理即可求解．
解答：解：五边形FGHIJ的内角和是：（5-2）×180=540°，
则∠γ=
=108°，
则∠β=180°-108°=72°，
∠α=180°-2×72°=36°．
则α：β：γ=36：72：108=1：2：3．
故答案是：1：2：3．
则∠γ=
| 540 |
| 5 |
则∠β=180°-108°=72°，
∠α=180°-2×72°=36°．
则α：β：γ=36：72：108=1：2：3．
故答案是：1：2：3．
点评：本题考查了多边形的内角和定理，正确求得∠γ的度数是关键．
练习册系列答案
阅读快车系列答案
相关题目
下列运算结果为正数的是（ ）
| A、-2012-2013 |
| B、（-1）2013 |
| C、（-1）×（-2013） |
| D、-1+（-2013） |
如图是某滑板俱乐部训练时的斜坡截面的示意图，该截面垂直于地面，出于安全因素考虑，俱乐部决定将训练的斜坡AB改造成FD，这时斜坡的倾角由45°降为30°，坡顶加宽的长度AF为1m，已知原斜坡面AB唱为6
如图，梯形ABCD中，AD∥BC，∠BAD=90°，AD=7cm，BC=4cm，AB=4cm，现有动点P以3cm/s的速度从点A向点D运动，动点Q以2cm/s的速度从点C向点B运动，若P，Q两点同时出发，一个点停止运动时另一个点也停止运动，连接AQ、PQ，设运动时间为x s，请问x为何值时，△APQ为等腰三角形．已知△ABC中，AB=AC，BC=8，其外接圆半径为5，则△ABC的周长为（ ）
A、8+4
| ||||
B、8+8
| ||||
C、8+4
| ||||
| D、以上都不对 |
下列四个图案中，可以通过如图平移得到的是（ ）A、 |
B、 |
C、 |
D、 |
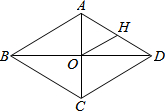如图所示，菱形ABCD中，对角线AC、BD相交于点O，H为AD边的中点，菱形ABCD的周长为36，则OH的长等于（ ）| A、4.5 | B、5 | C、6 | D、9 |
在锐角三角形ABC中，BC＞AB＞AC，小靖依下列方法作图：
（1）作∠A的平分线交BC于D点．
（2）作AD的中垂线交AC于E点．
（3）连接DE．
根据他画的图形，下列关系正确的是（ ）
（1）作∠A的平分线交BC于D点．
（2）作AD的中垂线交AC于E点．
（3）连接DE．
根据他画的图形，下列关系正确的是（ ）
| A、DE∥AB |
| B、DE⊥AC |
| C、CD=DE |
| D、CD=BD |