题目内容
11.已知:二次函数y=ax2+bx+6(a≠0)与x轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.(1)请直接写出点A、B的坐标,并求出该二次函数的解析式.
(2)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
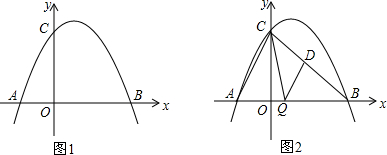
分析 (1)解一元二次方程求出两个根,然后写出A、B的坐标,再将点A、B代入抛物线求出a、b,即可得解;
(2)根据抛物线解析式求出点C的坐标以及对称轴,根据轴对称确定最短路线问题,直线BC与对称轴的交点即为所求的点P,然后求解即可;
(3)表示出BQ,然后求出△ABC和△QBD相似,再根据相似三角形的面积的比等于相似比的平方求出△BDQ的面积,然后根据S△CDQ=S△BCO-S△BDQ列式整理,再根据二次函数的最值问题求解.
解答 解:(1)因式分解得,(x+2)(x-6)=0,
所以,x+2=0,x-6=0,
解得x1=-2,x2=6,
所以A(-2,0),B(6,0),
将点A、B的坐标代入得,$\left\{\begin{array}{l}{4a-2b+6=0}\\{36a+6b+6=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
所以,二次函数的解析式为y=-$\frac{1}{2}$x2+2x+6;
(2)令x=0,则y=6,
所以,点C(0,6),
∵y=-$\frac{1}{2}$x2+2x+6=-$\frac{1}{2}$(x-2)2+8,
∴对称轴为直线x=2,
由轴对称确定最短路线问题,直线BC与对称轴的交点即为所求的点P,
设直线BC的解析式为y=kx+b,
则$\left\{\begin{array}{l}{6k+b=0}\\{b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
所以,直线BC的解析式为y=-x+6,
x=2时,y=-2+6=4,
所以,存在点P(2,4),使△APC的周长最小;
(3)∵点Q(m,0)是线段OB上一个动点,B(6,0),
∴BQ=6-m,
∵A(-2,0),(6,0),C(0,6),
∴AB=6-(-2)=8,OC=6,
∴S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×8×6=24,
∵QD∥AC,
∴△ABC∽△QBD,
∴$\frac{{S}_{△QBD}}{{S}_{△ABC}}$=($\frac{6-m}{8}$)2,
∴S△QBD=$\frac{(6-m)^{2}}{64}$×24=$\frac{3}{8}$(6-m)2,
∴S△CDQ=S△BCO-S△BDQ-S△COQ,
=$\frac{1}{2}$×6×6-$\frac{3}{8}$(6-m)2-3m,
=-$\frac{3}{8}$(2-m)2+6,
所以,当m=6时,△CDQ面积S最大,最大值为18.
点评 本题是二次函数综合题型,主要利用了一元二次方程的解法,待定系数法求二次函数解析式,轴对称确定最短路线问题,相似三角形的判定与性质,二次函数的最值问题,综合题但难度不大,难点在于(3)考虑利用相似三角形求解并表示出△CDQ的面积.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案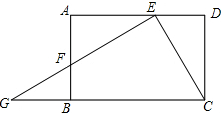 如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC交边AB于点F,交CB的延长线于点G,且EF=EC.
如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC交边AB于点F,交CB的延长线于点G,且EF=EC.(1)求证:CD=AE;
(2)若DE=6,矩形ABCD的周长为48,求CG的长.
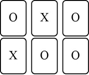 怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )
怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| 总收入/万元 | 总支出/万元 | 结余/万元 | |
| 前年 | x | y | x-y |
| 去年 | 1.2x | 1.15y | 1.2x-1.15y |
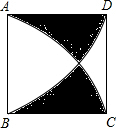 已知,如图,正方形ABCD是边长为1的正方形,分别以A、B为圆心,1为半径画弧,求阴影部分面积.
已知,如图,正方形ABCD是边长为1的正方形,分别以A、B为圆心,1为半径画弧,求阴影部分面积.


