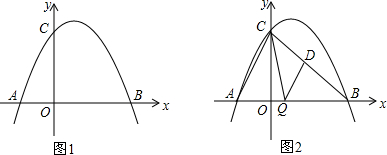题目内容
1.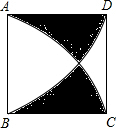 已知,如图,正方形ABCD是边长为1的正方形,分别以A、B为圆心,1为半径画弧,求阴影部分面积.
已知,如图,正方形ABCD是边长为1的正方形,分别以A、B为圆心,1为半径画弧,求阴影部分面积.
分析 如图,阴影ADE的面积可以看成是扇形ADE的面积减弓形的面积,弓形的面积可以看成扇形BAE的面积减三角形ABE的面积,阴影ADE的2倍即为所求.
解答 解:如图: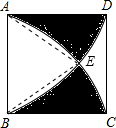 连接AE、BE
连接AE、BE
则△ABE是等边三角形,
∴AB=AE=BE=1,∠ABE=60°∠DAE=30°,
∴S扇形BAE=$\frac{60×π×{1}^{2}}{360}$=$\frac{π}{6}$
S扇形ADE=$\frac{30×π×{1}^{2}}{360}$=$\frac{π}{12}$
S△ABE=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$
∴S阴影=2[S扇形ADE-(S扇形BAE-S△ABE)]=2[$\frac{π}{12}$-($\frac{π}{6}-\frac{\sqrt{3}}{4}$)=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
点评 本题主要考查了扇形面积的计算,解决此类问题的关键是合理分解图形,把要求面积部分看做几个规则图形面积的和差.

练习册系列答案
相关题目
12. 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )| A. | 6m2 | B. | 21m2 | C. | 3m2 | D. | 5m2 |
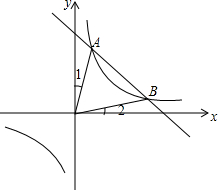 如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).
如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).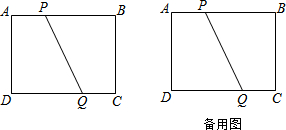
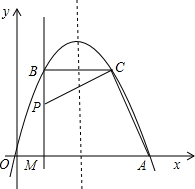 如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.
如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.
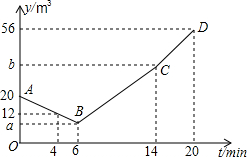 水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.