题目内容
18.计算:(1)-3$\sqrt{\frac{4}{3}}$÷2$\sqrt{\frac{3}{2}}$×$\sqrt{\frac{9}{8}}$
(2)($\sqrt{12}$-4$\sqrt{\frac{1}{3}}$)×$\sqrt{6}$.
(3)$\frac{3}{2}$$\sqrt{9m}$+6$\sqrt{\frac{m}{4}}$-2m$\sqrt{\frac{1}{m}}$
(4)$(\sqrt{3}+\sqrt{2})×(\sqrt{3}-\sqrt{2})$-${(3+2\sqrt{5})^2}$.
分析 (1)先将各二次根式化简,再将除法转化为乘法后统一相乘;
(2)运用乘法分配律将各根数相乘,再运用二次根式的性质化简;
(3)依据二次根式的性质将各二次根式化简,按照运算顺序先乘再加、减;
(4)根据平方差公式和完全平方公式先计算这里的乘法和乘方,再加减.
解答 解:(1)原式=-2$\sqrt{3}$÷$\sqrt{6}$×$\frac{3\sqrt{2}}{4}$
=-2$\sqrt{3}$×$\frac{\sqrt{6}}{6}$×$\frac{3\sqrt{2}}{4}$
=-$\frac{3}{2}$;
(2)原式=$\sqrt{72}$-4$\sqrt{2}$
=6$\sqrt{2}$-4$\sqrt{2}$
=2$\sqrt{2}$;
(3)原式=$\frac{9\sqrt{m}}{2}$+3$\sqrt{m}$-2$\sqrt{m}$
=$\frac{11\sqrt{m}}{2}$;
(4)原式=3-2-(9+12$\sqrt{5}$+20)
=1-9-12$\sqrt{5}$-20
=-28-12$\sqrt{5}$.
点评 本题主要考查二次根式的混合运算,熟练掌握二次根式的性质进行化简是根本也是关键,根据不同算式注意观察适时使用简便方法也很重要.

练习册系列答案
相关题目
3. 如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
 如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{7}$ |
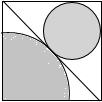 如图,在边长为a的大正方形的对角线一边作一个足够大的小圆,在另一边作一个足够大的四分之一圆,则这两个阴影部分的面积比为(3+2$\sqrt{2}$):4.
如图,在边长为a的大正方形的对角线一边作一个足够大的小圆,在另一边作一个足够大的四分之一圆,则这两个阴影部分的面积比为(3+2$\sqrt{2}$):4.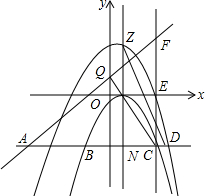 如图,已知过点(0,-$\frac{1}{4}$)的抛物线C1:y=ax2+bx+c的顶点为Q(1,0),现将该抛物线上所有点的纵坐标加h(h>0),横坐标不变,得到新的抛物线,记为C2,在y轴的负半轴作一条平行于x轴的直线,与两条抛物线交于A、B、C、D四点,直线AD与x轴的距离是m2(m>0)
如图,已知过点(0,-$\frac{1}{4}$)的抛物线C1:y=ax2+bx+c的顶点为Q(1,0),现将该抛物线上所有点的纵坐标加h(h>0),横坐标不变,得到新的抛物线,记为C2,在y轴的负半轴作一条平行于x轴的直线,与两条抛物线交于A、B、C、D四点,直线AD与x轴的距离是m2(m>0)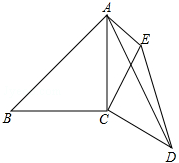 如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.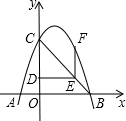 如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.
如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F. 如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角∠1为30°,则飞机A与指挥台B的距离为2400m.
如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角∠1为30°,则飞机A与指挥台B的距离为2400m. 如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=140°;若∠A=n°,则∠BEC=90°+$\frac{1}{2}$n°.
如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=140°;若∠A=n°,则∠BEC=90°+$\frac{1}{2}$n°.