Question

9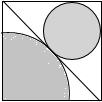．如图，在边长为a的大正方形的对角线一边作一个足够大的小圆，在另一边作一个足够大的四分之一圆，则这两个阴影部分的面积比为（3+2$\sqrt{2}$）：4．

Answer 1

分析 连接BD交AC于O，设小圆的半径为r，由正方形的性质得出PD=$\sqrt{2}$r，BO=DO=r+$\sqrt{2}$r，求出扇形的面积，即可得出结果．

解答 解：如图所示：
连接BD交AC于O，作PM⊥CD于M，
设小圆的半径为r，则PD=$\sqrt{2}$r，
∴BO=DO=r+$\sqrt{2}$r，
∴扇形的面积=$\frac{1}{4}$π•（r+$\sqrt{2}$r）²=$\frac{3+2\sqrt{2}}{4}$πr²，
∴扇形面积：小圆面积=$\frac{3+2\sqrt{2}}{4}$πr²：πr²=（3+2$\sqrt{2}$）：4；
故答案为：（3+2$\sqrt{2}$）：4．

点评 本题考查了正方形的性质、扇形面积的计算、圆的面积公式；熟练掌握正方形的性质，得出扇形和圆的面积关系是解决问题的关键．