题目内容
13.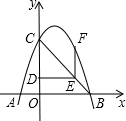 如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.
如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.(1)求此抛物线的解析式;
(2)小明在探究点D运动时发现,①当点D与点C重合时,EF长度可看作O;②当点D与点O重合时,EF长度也可以看作O,于是他猜想:设点D运动到OC中点位置时,当线段EF最长,你认为他猜想是否正确,为什么?
(3)连接CF、DF,请直接写出△CDF为等腰三角形时所有t的值.
分析 (1)由于已知抛物线与x轴交点坐标,则设交点式y=a(x+1)(x-3),然后把C点坐标代入求出a即可得到抛物线解析式;
(2)先利用待定系数法求出直线BC的解析式,再设E(t,-t+3),接着表示出D(0,-t+3),F(t,-t2+2t+3),然后用t表示出EF的长,再利用二次函数的性质确定EF最大时的t的值,从而判断点D是否为OC的中点;
(3)先由C(0,3),D(0,-t+3),F(t,-t2+2t+3)和利用两点间的距离公式表示出CD2,CF2,DF2,然后分类讨论:当CD=CF或FC=FD或DC=DF时得到关于t的方程,接着分别解关于t的方程即可.
解答  解:(1)设抛物线的解析式为y=a(x+1)(x-3),
解:(1)设抛物线的解析式为y=a(x+1)(x-3),
把C(0,3)代入得a•1•(-3)=3,解得a=-1,
所以抛物线解析式为y=-(x+1)(x-3),即y=-x2+2x+3;
(2)他猜想正确.理由如下:
设直线BC的解析式为y=mx+n,
把C(0,3),B(3,0)代入得$\left\{\begin{array}{l}{n=3}\\{3m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=3}\end{array}\right.$,则直线BC的解析式为y=-x+3,
设E(t,-t+3),则D(0,-t+3),F(t,-t2+2t+3),
所以EF=-t2+2t+3-(-t+3)=-t2+3t=-(t-$\frac{3}{2}$)2+$\frac{9}{4}$,
当t=$\frac{3}{2}$时,EF最大,最大值为$\frac{9}{4}$,
此时D点坐标为(0,$\frac{3}{2}$),
所以点D为OC的中点时,线段EF最长;
(3)∵C(0,3),D(0,-t+3),F(t,-t2+2t+3),
∴CD2=(-t+3-3)2=t2,CF2=t2+(-t2+2t+3-3)2=t2+(-t2+2t)2,DF2=t2+(-t2+2t+3+t-3)2=t2+(-t2+3t)2,
当CD=CF时,即t2=t2+(-t2+2t)2,解得t1=0,t2=2;
当FC=FD,即t2+(-t2+2t)2=t2+(-t2+3t)2,解得t1=0,t2=$\frac{5}{2}$;
当DC=DF时,即t2=t2+(-t2+3t)2,解得t1=0,t2=3;
综上所述,当t=2或$\frac{5}{2}$或3时,△CDF为等腰三角形.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质;会运用待定系数法求一次函数和二次函数的解析式;会利用分类讨论的思想解决数学问题;理解坐标与图形的性质,记住两点间的距离公式.

 星级口算天天练系列答案
星级口算天天练系列答案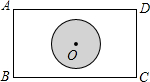 如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )
如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )| A. | 300m | B. | 400m | C. | 500m | D. | 600m |
| A. | -1 | B. | 6 | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
 如图,△ABC中,∠ABC=40°,BD平分∠ABC,BC=BD+AD.求证:AB=AC.
如图,△ABC中,∠ABC=40°,BD平分∠ABC,BC=BD+AD.求证:AB=AC.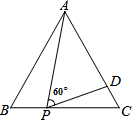 如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,
如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,