题目内容
8.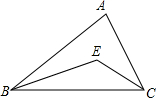 如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=140°;若∠A=n°,则∠BEC=90°+$\frac{1}{2}$n°.
如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=140°;若∠A=n°,则∠BEC=90°+$\frac{1}{2}$n°.
分析 根据三角形的内角和定理和角平分线的定义求得.
解答 解:∵在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=80°.
∴∠EBC+∠ECB=$\frac{180°-80°}{2}$=40°,
∴∠BEC=180°-40°=140°;
∵在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=n°.
∴∠EBC+∠ECB=$\frac{180°-n°}{2}$=90°-$\frac{1}{2}$n°,
∴∠BEC=180°-(90°-$\frac{1}{2}$n°)=90°+$\frac{1}{2}$n°.
故答案为:140°,90°+$\frac{1}{2}$n°.
点评 本题考查了角平分线的定义,三角形的内角和,熟记三角形的内角和是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
20.下列函数中,为一次函数的是( )
| A. | $y=\frac{1}{x}+1$ | B. | y=-2x | C. | y=x2+1 | D. | y=kx+1(k是常数) |
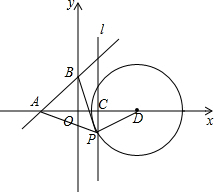 如图,直线y=x+b(b>0)与x、y轴分别相交于A、B两点,点C(1,0),过点C作垂直于x轴的直线l,在直线l上取一点P,满足PA=PB,点A关于直线l的对称点为点D,以D为圆心,DP为半径作⊙D.
如图,直线y=x+b(b>0)与x、y轴分别相交于A、B两点,点C(1,0),过点C作垂直于x轴的直线l,在直线l上取一点P,满足PA=PB,点A关于直线l的对称点为点D,以D为圆心,DP为半径作⊙D.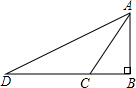 如图,某人要测一建筑物AB的高度,他在地面D处测得建筑物顶端A的仰角为30°,沿AE方向前进100米到达点C处,测得建筑物的顶端A的仰角为45°,求建筑物的高.
如图,某人要测一建筑物AB的高度,他在地面D处测得建筑物顶端A的仰角为30°,沿AE方向前进100米到达点C处,测得建筑物的顶端A的仰角为45°,求建筑物的高.