题目内容
17.A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )| A. | $\frac{180}{x}$-$\frac{180}{(1+50%)x}$=1 | B. | $\frac{180}{(1+50%)x}$-$\frac{180}{x}$=1 | ||
| C. | $\frac{180}{x}$-$\frac{180}{(1-50%)x}$=1 | D. | $\frac{180}{(1-50%)x}$-$\frac{180}{x}$=1 |
分析 直接利用在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h,利用时间差值得出等式即可.
解答 解:设原来的平均车速为xkm/h,则根据题意可列方程为:
$\frac{180}{x}$-$\frac{180}{(1+50%)x}$=1.
故选:A.
点评 此题主要考查了由实际问题抽象出分式方程,根据题意得出正确等量关系是解题关键.

练习册系列答案
相关题目
5.化简:$\frac{{a}^{2}-4}{{a}^{2}+2a+1}$÷$\frac{{a}^{2}-4a+4}{(a+1)^{2}}$-$\frac{2}{a-2}$的结果为( )
| A. | $\frac{a+2}{a-2}$ | B. | $\frac{a-4}{a-2}$ | C. | $\frac{a}{a-2}$ | D. | a |
6.二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
7. 为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
(1)填空:a=10,b=28%;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
 为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:频数分布表
| 身高分组 | 频数 | 百分比 |
| x<155 | 5 | 10% |
| 155≤x<160 | a | 20% |
| 160≤x<165 | 15 | 30% |
| 165≤x<170 | 14 | b |
| x≥170 | 6 | 12% |
| 总计 | 100% |
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
 如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.
如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.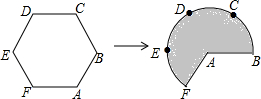 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18.
如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=120°.
如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=120°.